# 前置知识
- 高中函数和三角变换部分
- 高等数学(微分表、积分表)
- 线性代数
- 数学物理方法(本科阶段通常是复变函数和微分方程)
- 一点概率论(知道啥是概率密度)
- 五小力学、分析力学、电动力学、热统(非物理科班:大学物理学)
- 教材相关
# 球坐标下拉普拉斯算符的表示
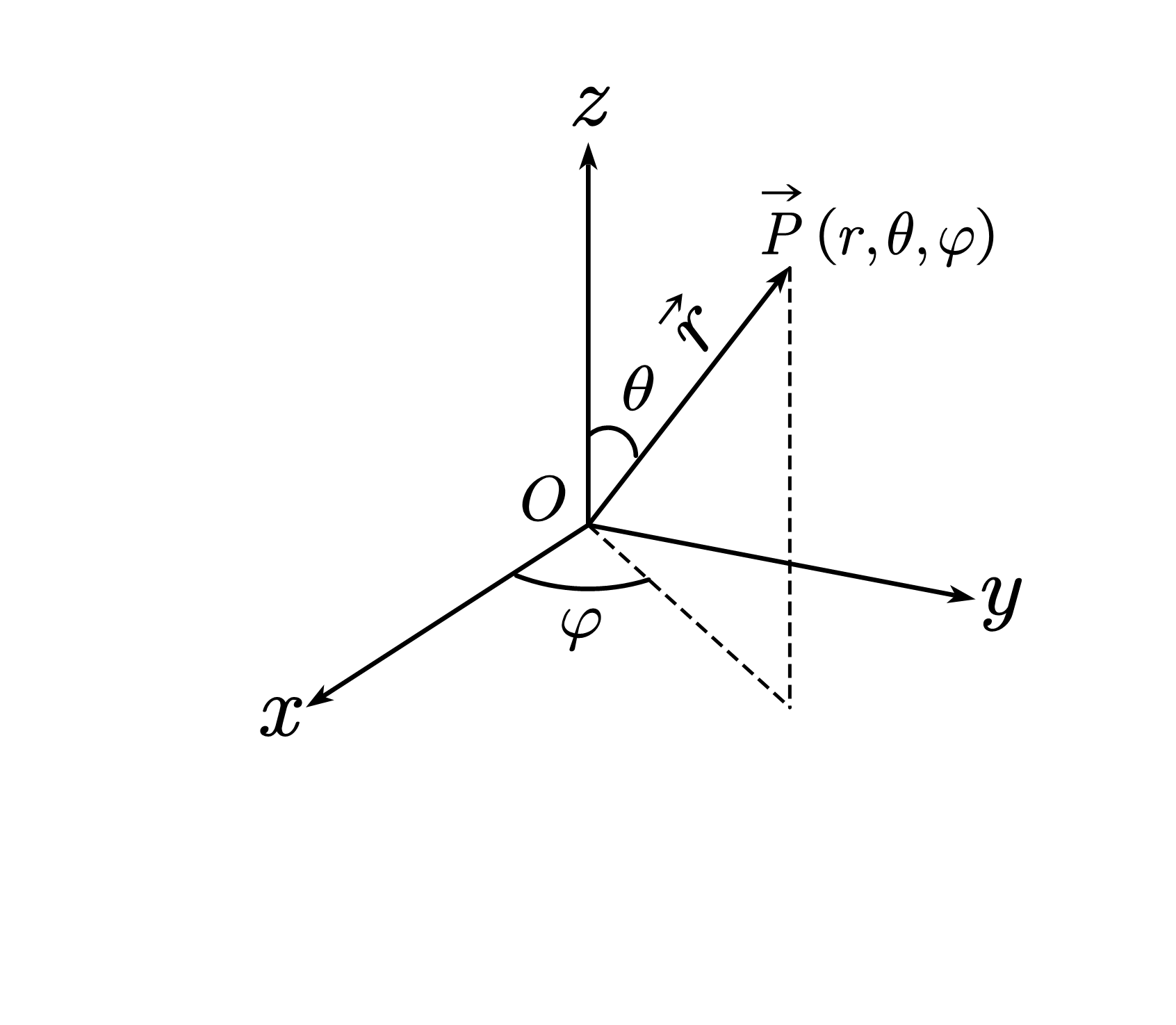
![图1 球坐标系 球坐标系]()
球坐标与直角坐标的关系:
x=rsinθcosφ,y=rsinθsinφ,z=rcosθ
r=x2+y2+z2,θ=arctan2x2+y2,φ=arctanxy
哈密顿算子(Nabla 算子):
∇=∂x∂i+∂y∂j+∂z∂k=e^r∂r∂+e^θr1∂θ∂+e^φrsinθ1∂φ∂
拉普拉斯算符:
∇2=∂x2∂2+∂y2∂2+∂z2∂2=∂r2∂2+r21∂r2∂2+r2∂r∂+r21sinθcosθ∂θ∂+r2sin2θ1∂φ2∂2=r21∂r∂r2∂r∂+r2sinθ1∂θ∂sinθ∂θ∂+r2sin2θ1∂φ2∂2
# 柱坐标下拉普拉斯算符的表示
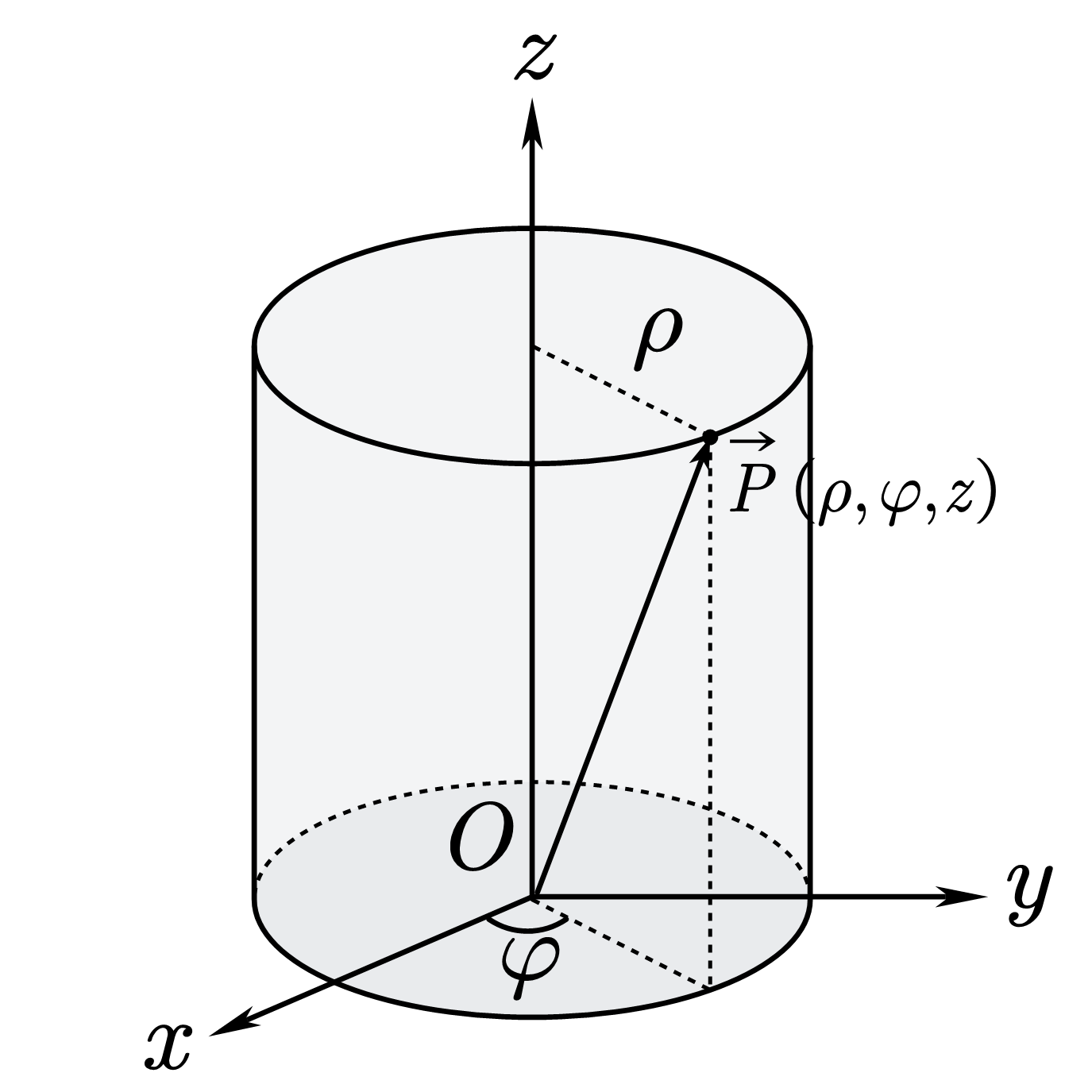
![图2 柱坐标系 柱坐标系]()
柱坐标与直角坐标的关系:
x=ρcosφ,y=ρsinφ,z=z
x2+y2=ρ2,xy=tanφ,z=z
哈密顿算子(Nabla 算子):
∇=∂x∂i+∂y∂j+∂z∂k=e^ρ∂ρ∂+e^φρ1∂φ∂+e^z∂z∂
拉普拉斯算符:
∇2=∂x2∂2+∂y2∂2+∂z2∂2=∂ρ2∂2+ρ1∂ρ∂+ρ21∂φ2∂2+∂z2∂2=ρ1∂ρ∂ρ∂ρ∂+ρ21∂φ2∂2+∂z2∂2
# 狄拉克 δ 函数
# 定义
Dirac 引入 δ 函数定义,对于多维空间中:
δ(x)=⎩⎪⎨⎪⎧∞,0,x=0x=0且∫−∞∞δ(x)dx=1
δ 函数在数学上可以通过分布理论严格化。δ 函数又叫脉冲函数,它是一个广义函数(泛函)。
![图3 狄拉克 δ 函数 狄拉克 δ 函数]()
# δ 函数的几种表达方式
实际应用中,δ 函数常用某些函数的极限形式表达。
- δ→0lim2πδ1e−2δx2=δ(x)
- α→∞limπxsinαx=δ(x)
- 2π1∫−∞∞eikxdk=δ(x) 或者2π1∫−∞∞e−ikxdx=δ(k)
- σ→0+limπ1x2+ϵ2ϵ=δ(x)
- 2π1∫−∞∞ei(k−k′)xdr=δ(k−k′)
- 2πℏ1∫−∞∞eℏi(p−p′)xdx=δ(p−p′)(一维)
- (2πℏ)31∫−∞∞eℏi(p−p′)rdr=δ(p−p′)(三维)
# δ 函数的性质
对称性( δ 函数是偶函数):δ(−x)=δ(x)
挑选性(筛选性)
对于任何连续函数 f(x) :
∫∞−∞f(x)δ(x−a)dx=f(a)
特别地,当 a=0 时,∫∞−∞f(x)δ(x)dx=f(0)
有一个 δ(x) 脱去一个积分号 ∫ 或求和号 ∑
放缩或相似性:
δ(ax)=∣a∣1δ(x)
φ(x) 是一个二次以上可导函数。设 {xi} 为其单零点的集合,即在任意一点 xi 处,我们有 φ(xi)=0 ,φ′(xi)=0 ,那么有:
δ(φ(x))=i∑N∣φ′(xi)∣δ(x−xi)
∫Rnf(x)[∇δ(x−a)]dx=−∇f(x)∣x=a
位矢的微分:
∇⋅r3r=−∇2(r1)=4πδ(r)
# 矢量分析
∇(A⋅v)=(A⋅∇)v+(v⋅∇)A+A×(∇×v)+v×(∇×A)
∇=∂x∂i+∂y∂j+∂z∂k
∇2=∇⋅∇=∇(∂x∂i+∂y∂j+∂z∂k)=∂x2∂2+∂y2∂2+∂z2∂2
# 无穷级数
函数直接展开为 x 的幂级数:
求 f(x) 的各阶导数 f′(x),f′′(x),⋯,f(n)(x),⋯;
求出函数及其各阶导数在 x=0 处的值 f(0),f′(0),f′′(0),⋯,f(n)(0),⋯;
写出幂级数 f(0)+f′(0)x+2!f′′(0)x2+⋯+n!f(n)(0)xn+⋯ ,并求出收敛半径:R=limn→∞∣∣∣∣an+1an∣∣∣∣;
验证余项 n→∞limRn(x)=n→∞lim(n+1)!1f(n+1)(θx)xn+1 是否为零,如果为零,则函数 f(x) 在区间 (−R,R) 的幂级数展开式为:
f(x)=f(0)+f′(0)x+2!f′′(0)x2+⋯+n!fn(0)xn+⋯,x∈(−R,R)
f(x) 在 x0 点的泰勒级数:
f(x)=n=0∑∞n!1f(n)(x0)(x−x0)n,x∈U(x0)
当 x0=0 时,级数
f(x)=n=0∑∞n!1f(n)(0)xn
称为麦克劳林级数。
如果 f(x) 在 U(x0) 内具有各阶导数,则
f(x)=n=0∑∞n!1f(n)(x0)(x−x0)n⟺n→∞limRn(x)=0
常见函数的泰勒级数:
- cosα=n=0∑∞(2k)!(−1)kα2k,n=0,2,4,…
- sinα=n=1∑∞(2k+1)!(−1)kα2k+1,n=1,3,5,…
- ex=n=0∑∞n!xn
- ax=exlna=n=0∑∞n!(lna)nxn
- ln(1+x)=n=1∑∞(−1)n−1nxn,x∈(−1,1]
- (1+x)m=n=1∑∞n!m(m−1)⋯(m−n+1)xn,x∈(−1,1)
- 1−x1=n=0∑∞xn,x∈(−1,1)
- arctanx=n=0∑∞2n+1(−1)nx2n+1,x∈[−1,1]
# 补充
# 三角变换
sin(α±β)=sinαcosβ±cosαsinβ
cos(α±β)=cosαcosβ∓sinαsinβ
# 其它
∫0∞xne−ax=an+1n!
高斯积分公式:
∫−∞∞e−ax2dx=an
或者
∫0∞x2ne−ax2dx=2n+1an1⋅3⋅5⋯(2n−1)an
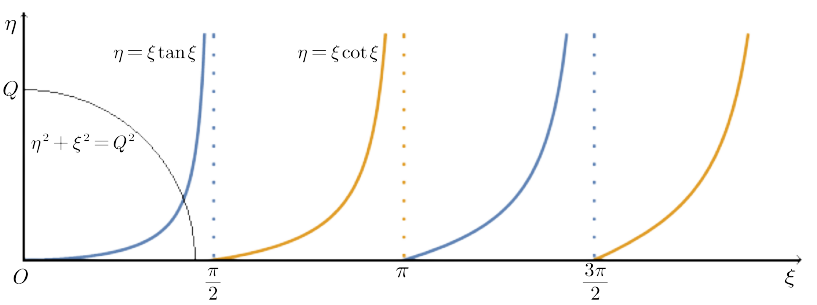
η=ξtanξ 与 ξ2+η2=Q2:
![图4 η=ξtgξ、η=ξctgξ η=ξtgξ、η=ξctgξ]()
# 参考资料