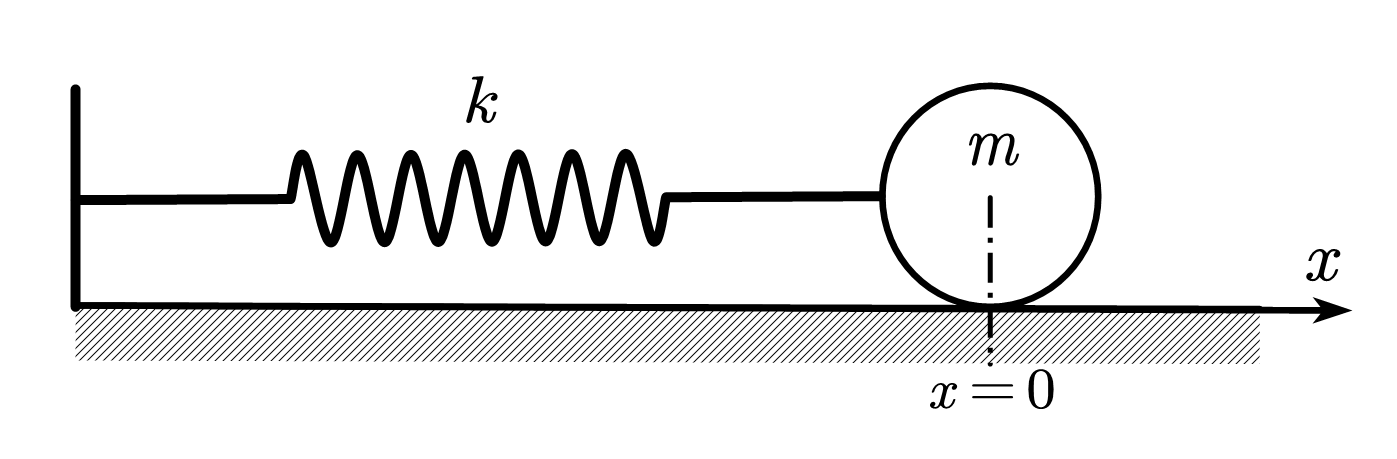
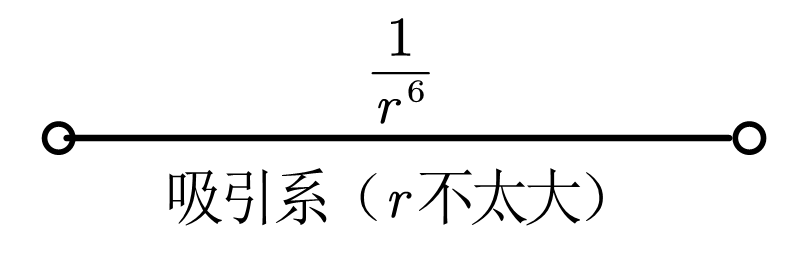# 一维谐振子
![图1-1 弹簧振子 图1-1 弹簧振子]()
力:F(x)=−kx
势函数:V(x)=21kx2=21mkmx2=21ω02mx2
弹簧振子的固有角频率:ω02=mk
Schrödinger 解法:
一维谐振子势函数:V(x)=21ω02mx2
相应 Schrödinger 方程:
iℏ∂t∂ψ(x,t)=−2mℏ2∂x2∂2ψ(x,t)+21ω02mx2ψ(x,t)
使用分离变量法,把 t 分离出来
令 ψ(x,t)=ϕ(x)e−iωt ,ω 为待定系数
Schrödinger 方程改写为
iℏ(−iω)ϕ(x)e−iωt=[−2mℏ2dx2d2ϕ(x)+21mω02x2ϕ(x)]e−iωt
ℏωϕ(x)=Eϕ(x)=−2mℏ2dx2d2ϕ(x)+21mω02x2ϕ(x)
化为解微分方程的定态问题
dx2d2ϕ(x)+ℏ22m(E−21mω02x2)ϕ(x)=0
奇异点分析:
当 ∣x∣→∞ 时,V(x)→∞ ,粒子为束缚态。∣x∣→∞limφ(x)=0
−2mℏ2dx2d2ϕ(x)+21mω02x2ϕ(x)≅0
令方程解为 ϕ~=eλx ,则 ϕ′=λeλx ,ϕ′′=λ2eλx
−2mℏ2λ2eλx+21mω02x2eλx=0
则
λ=±ℏmω0x
ϕ~=exp(±2ℏmω0x2)
dxdϕ~(x)=exp(−2ℏmω0x2)(−ℏmω0x)
dx2d2ϕ~(x)=exp(−2ℏmω0x2)(−ℏmω0x)2−ℏmω0exp(−2ℏmω0x2)
代入渐近方程:
−2mℏ2dx2d2ϕ~(x)+21mω02x2ϕ~(x)=[−2mℏ2(ℏmω0x)2−ℏmω0(−2mℏ2)]exp(−2ℏmω0x2)+21mω02x2exp(−2ℏmω0x2)≅(−21mω02x2+21mω02x2)exp(−2ℏmω0x2)=0
推得
−2mℏ2dx2d2ϕ~(x)+21mω02x2ϕ~(x)≅0
解得
ϕ~1=exp(−2ℏmω0x2),ϕ~2=exp(2ℏmω0x2)(x→∞,是发散的,舍弃)
我们要求波函数是平方可积的,所以要求 x→∞ ,波函数一定趋近于 0
令
ϕ(x)=ϕ~(x)χ(x)=exp(−2ℏmω0x2)χ(x)
ϕ′(x)=−ℏmω0xexp(−2ℏmω0x2)χ(x)+exp(−2ℏmω0x2)χ′(x)
ϕ′′(x)=[(ℏmω0x)2−ℏmω0]exp(−2ℏmω0x2)χ(x)−ℏ2mω0xexp(−2ℏmω0x2)χ′(x)+exp(−2ℏmω0x2)χ′′(x)
代入
−2mℏ2ϕ′′(x)+21mω02x2ϕ(x)=Eϕ(x)
−2mℏ2[(ℏmω0x)2−ℏmω0]exp(−2ℏmω0x2)χ(x)+21mω02x2exp(−2ℏmω0x2)χ(x)−ℏ2mω0xexp(−2ℏmω0x2)χ′(x)=Eexp(−2ℏmω0x2)χ(x)+exp(−2ℏmω0x2)χ′′(x)
−2mℏ2χ′′(x)+ℏω0xχ′(x)+21ℏω0χ(x)−21mω02x2χ(x)+21mω02x2χ(x)=Eχ(x)
2mℏ2χ′′(x)−ℏω0xχ′(x)+(E−21ℏω)χ(x)=0(福克斯Fuchs微分方程)
奇异点分析做完,把奇异点扣除,由于方程是二阶的,所以一定有两个线性无关的解在零点处解析(可在零点展成无穷级数)
χ(x)χ′(x)χ′′(x)=C0+C1x+C2x2+⋯=C1+2C2x+3C3x2+⋯=2C2+6C3x+⋯
2mℏ2χ′′−ℏω0xχ′+(E−21ℏω)χ=0
2mℏ2(2C2+6C3x+⋯)−ℏω0x(C1+2C2x+3C3x2+⋯)+(E−21ℏω)(C0+C1x+C2x2+⋯)=0
展开每项
2mℏ2⋅2C2+(E−21ℏω)C0+2mℏ2⋅6C3x+⋯−ℏω0xC1−ℏω0x⋅2C2x+⋯+(E−21ℏω)C1x+(E−21ℏω)C2x2+⋯=0
x 的一次幂、二次幂、三次幂作为函数是线性无关的,若其线性关系等于 0 ,则所乘系数必须等于 0 。
x0x1x2=2mℏ2⋅2C2+(E−21ℏω)C0=0=2mℏ2⋅6C3−ℏω0xC1+(E−21ℏω)C1=0=−ℏω0x⋅2C2+(E−21ℏω)C2=0⋮
C0 和 C1 不确定(有一定自由度),一旦给定,其余系数也都能给定。
- 取 C0=1 ,C1=0 ,则 C1=C3=C5=⋯=0
2mℏ2⋅2C2=−(E−21ℏω)⇓C2=−ℏm(E−21ℏω)C0=−(E−21ℏω),C4=0,C6=0
χ偶(x)=C0+C2x2+C4x4+⋯
当∣x∣→∞,χ偶(x)=exp(−ℏmω0x2)
ϕ(x)=exp(−2ℏmω0x2)χ偶(x)∣x∣→∞{exp(−2ℏmω0x2)exp(ℏmω0x2)exp(2ℏmω0x2)(发散需截断)
令 E−21ℏω=0 ,E0=21ℏω ,则 C2=0,C4=0,C6=0,⋯
χ0(x)=C0+C2x2+C4x4+⋯=C0=1
ϕ(x)=A0exp(−2ℏmω0x2)χ0(x)=A0exp(−2ℏmω0x2),A0为归一化系数。
- 取 C0=0 ,C1=1 则 C0=C2=C4=⋯=0
m3ℏ2C3=−(E−23ℏω)E=23ℏω(需截断否则发散)
C3=0,C5=0,⋯
χ1(x)=x
结论:当 E 取值为 En=(n+21)ℏω0 ,n=0,1,2,⋯ 时,χ(x) 的级数解会在某一阶截断,成为厄密多项式 Hn(y)(为实函数),χn(x)=Hn(y)=Hn(ℏmω0x) 。
ϕn(x)=Anexp(−2ℏmω0x2)Hn(ℏmω0x),An=[π2nn!ℏmω0]21
引入归一化系数 An ,使得波函数归一化,即
ϕn(x)=Anexp(−2ℏmω0x2)Hn(ℏmω0x),An=[π2nn!ℏmω0]21
∫−∞∞ϕn∗(x)ϕn(x)dx=∫−∞∞∣ϕn(x)∣2dx=1
(ϕm,ϕn)=∫−∞∞ϕm∗(x)ϕn(x)dx=0(若m=n)
∫−∞∞ϕm∗(x)ϕn(x)dx=δmn
引入记号 α=ℏmω0
ϕ0(x)=π1/4αe−2α2x2,ϕ1(x)=π1/42ααxe−2α2x2,ϕ2(x)=π1/4α/2(2α2x2−1)e−2α2x2,E0=21ℏω0E1=23ℏω0E2=25ℏω0⎭⎪⎪⎪⎬⎪⎪⎪⎫En=(n+21)ℏω0
E0=21ℏω0 为零点能。
估算:
x∼0⇒xˉ∼(Δx)2,Px∼0⇒Px∼(ΔPx)2
xˉ⋅Px∼(Δx)2(ΔPx)2∼41ℏ2=21ℏ
⇒xˉ=2ℏPx1
E≅2mP2+21mω02xˉ2=2mP2+21mω024ℏ2P21
令 t=P2 ,
dtdE(t)=2m1+81mω02ℏ2(−t21)=0
2m1=−81mω02ℏ2(t21)
⇒t2=(21mω0ℏ)2⇒tmin=21mω0ℏ
Emin=E(tmin)=2mtmin+21mω024tminℏ2=2m12mω0ℏ+21mω0242mω0ℏℏ2=41ℏω0+41ℏω0=21ℏω0
# 一维定态体系的一些基本性质
定理一
设势能函数 V(x) 为实函数。若 ψ(x) 是本征方程的解,则 ψ∗(x) 也是一个解,对应本征值也是 E(也适用于二维)。
证明:
若V∗(x)=V∗(x),即V∗(x)为实函数
Eψ(x)=−2mℏ2dx2d2ψ(x)+V(x)ψ(x)
[Eψ(x)]∗=Eψ∗(x)=[−2mℏ2dx2d2ψ(x)+V(x)ψ(x)]∗=−2mℏ2dx2d2ψ∗(x)+V(x)ψ∗(x)
推论
若方程的本征值 E 是非简并的,则相应的本征函数可以取作实函数。
非简并就是方程只有一个线性无关的解,一定有 ψ∗(x)=Cψ(x) ,
∫∣ψ∗(x)∣2dx=∫∣Cψ(x)∣2dx=∣C∣2∫∣ψ(x)∣2dx
假设 ∫∣ψ(x)∣2dx=1 ,因 ∫∣ψ∗(x)∣2dx=1 ,则 ∣C∣2=1 ,C=eiα ,ψ∗=ψ∣eiα∣2 。
定理二
设势能函数 V(x) 为实函数,则对应于任何方程的本征值 E ,总可以找到方程的一组实函数解。凡是属于本征值 E 的任何一个解,都可以表示成这组实函数解的线性叠加。
假设 ψ(x),ψ∗(x) 线性无关,即 C1ψ(x)+C2ψ∗(x)=0 ,则只有 C1=0,C2=0
定义 φ(x)=ψ(x)+ψ∗(x),χ(x)=−i[ψ(x)−ψ∗(x)](两函数都是实的,取复共轭等于其自身)
假设 D1φ+D2χ=0
D1[ψ(x)+ψ∗(x)]+D2{−i[ψ(x)−ψ∗(x)]}D1ψ+D1ψ∗−iD2ψ+iD2ψ∗(D1−iD2)ψ+(D1+iD2)ψ∗=0=0=0
因为 ψ,ψ∗ 线性无关,则
{D1−iD2=0D1+iD2=0⇒{D1=0D2=0
定理三
设势能函数 V(x) 具有空间反射对称性( V(−x)=V(x) )。若 ψ(x) 是方程的一个解,则 ψ(−x) 亦是该方程的一个解。
证明:令 x′=−x ,
Eψ(−x)=−2mℏ2dx2d2ψ(−x)+V(x)ψ(−x)=−2mℏ2dx2d2ψ(x′)+V(−x′)ψ(x′)⇓V(x)具有空间反射对称性。=−2mℏ2dx2d2ψ(x′)+V(x′)ψ(x′)=Eψ(x′)
当 E 为非简并时,有 P^ψn(x)=ψn(−x)=Cψ(x)
经过两次反射后,P^(P^ψ(x))=P^(ψ(−x))=P^(Cψ(x))=C2ψ(x)
因此 C2=1 或 C=±1 ,C 为波函数的宇称值,P^ 称为宇称算符。
若 P^ψn(x)=ψn(−x) ,则称 ψn(x) 具有偶宇称;若 P^ψn(x)=−ψn(x) ,则称 ψn(x) 具有奇宇称。
对于一维谐振子,由于它的每一条能级都是非简并的,因此相应的本征函数都具有确定的宇称。En=(n+21)ℏω0 ,P^φn(x)=φn(−x)=(−1)nφn(x) 。
定理四
设势能函数 V(x) 具有空间反射对称性。则对应于任何一个本征值 E ,我们总可以找到方程的一组解,它们的每一个都具有确定的宇称。而且,任何对应于本征值 E 的解 ψ(x) 都可以按照它们来展开。
证明:ψ(−x)=Cψ(x),ψ(x) 和ψ(−x) 是线性无关的,即 C1ψ(x)+C2ψ(−x)=0(C1=0,C2=0)
定义
ϕ(x)ϕ(−x)=ψ(x)+ψ(−x)=ψ(−x)+ψ(−(−x))=ψ(−x)+ψ(x)=ϕ(x)
ϕ(x) 和ϕ(−x) 也是线性无关的,上面看出 ϕ(x) 具有偶宇称。
而在定理二的证明中,χ(−x)=ψ(−x)−ψ(−(−x))=ψ(−x)−ψ(x)=−χ(x),即χ(x) 具有奇宇称。
定理五
对于一维空间的 Schrödinger 方程,若 ψ1(x) 和 ψ2(x) 是对应于同一本征值 E 的两个解,则有 ψ1(x)ψ2′(x)−ψ1′(x)ψ2(x)=常数。
证明:
{Eψ1(x)=−2mℏ2dx2d2ψ1(x)+V(x)ψ1(x)Eψ2(x)=−2mℏ2dx2d2ψ2(x)+V(x)ψ2(x)(1)(2)
(1)×ψ2(x)−(2)×ψ1(x) 得
−2mℏ2[ψ2(x)dx2d2ψ1(x)−ψ1(x)dx2d2ψ2(x)]=0
从方程中得
dxd[ψ1(x)ψ2′(x)−ψ1′(x)ψ2(x)]=0
因此
ψ1(x)ψ2′(x)−ψ1′(x)ψ2(x)=常数(仅一维空间)
定理六
假设粒子在一个一维空间中规则(即没有奇异点)的势函数 V(x) 中运动,则其束缚态必为非简并的。
证明:势函数 V(x) 为规则的 ⇒ Schrödinger 方程的任何一个解 ψ(x) 及其一阶导数 ψ′(x) 在空间的每一点都连续。
V(x)没有太多奇异性(regular)⇒{(1)不包含δ函数(2)V(x)有有限个阶跃
假设 En 是粒子的一个束缚态的本征值且简并,则可以找到至少两个本征函数 ψ1(x) 和 ψ2(x) 与它对应。
另一方面根据定理五,有
ψ1(x)ψ2′(x)−ψ1′(x)ψ2(x)=常数
对于束缚态,有渐进关系
∣x∣→∞limψ1(x)=∣x∣→∞limψ2(x)=0
则常数为零,方程改写为
ψ1(x)ψ1′(x)ψ11dxdψ1dxdlnψ1lnψ1或ψ1(x)=ψ2(x)ψ2′(x)=ψ21dxdψ2=dxdlnψ2=lnψ2+C=eCψ2(x)=Aψ2
即 ψ1(x) 与 ψ2(x) 线性相关,这与假设不符,因此得证。
总结:
⎩⎪⎪⎨⎪⎪⎧(1)定理一、二:势函数为实函数的情况;(2)定理三、四:势函数具有空间反射对称性的情况;(3)定理五、六:仅适用于一维空间,高维空间不成立。
# 一维方势阱
在量子力学中,一般给定势能函数较复杂,实际中可以近似于方势阱,其结果在定性上与真实出入不大。
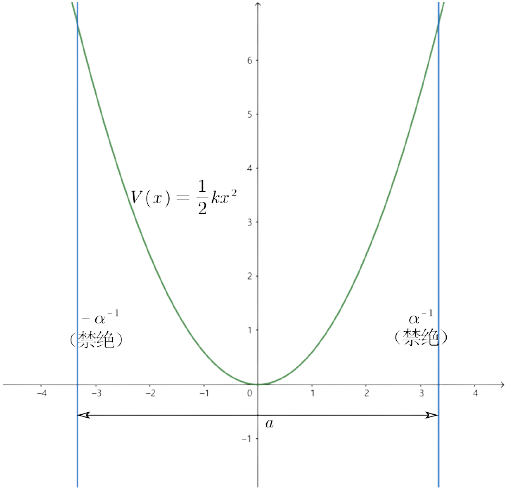
![图3-1 一维谐振子势函数 图3-1 一维谐振子势函数]()
V(x)=21kx2
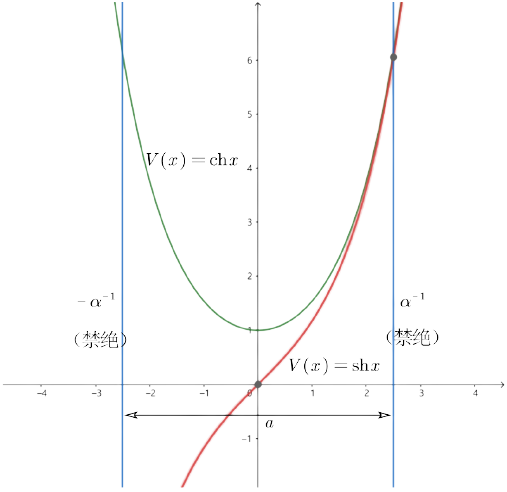
![图3-2 双曲余弦势函数 图3-2 一维谐振子势函数]()
V(x)=chx=2ex+e−x
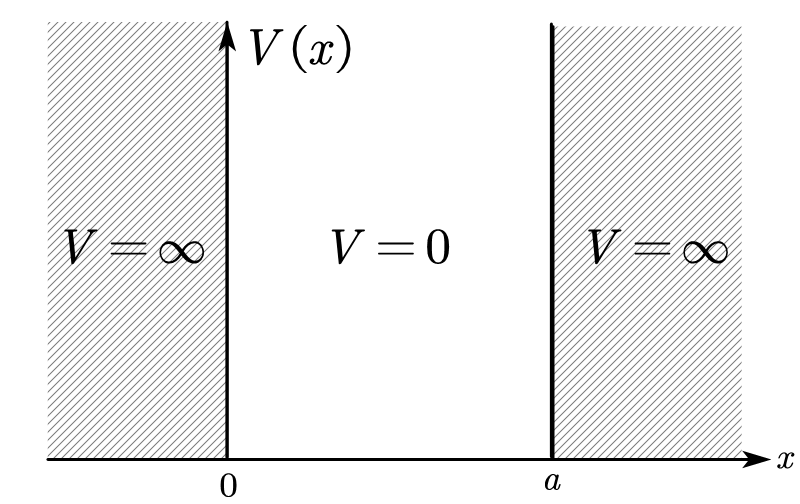
# 无穷深一维方势阱
对于一维谐振子、双曲余弦函数的近似。
![图3-3 图3-3]()
V(x)=⎩⎪⎪⎨⎪⎪⎧+∞,0,−∞,x⩽00⩽x⩽ax⩾a
阱内:
Eψ(x)=−2mℏ2dx2d2ψ(x)
阱外:令 ψ(x=0)=0 ,ψ(x=a)=0
Eψ(x)+2mℏ2dx2d2ψ(x)dx2d2ψ(x)+ℏ22mEψ(x)=0=0
令解 ψ=eλx ,ψ′=λeλx ,ψ′′=λ2eλx
λ2eλxλ+ℏ22mEeλx=0=−ℏ22mE
解得:
ψ1=exp(−iℏ22mEx),ψ2=exp(iℏ22mEx)
因为 ψ1(x=0)=1 ,ψ1(x=a)=exp(−iℏ22mEx)=0
ψ1 和 ψ2 线性无关,取其线性组合(原因:Schrödinger 方程是线性的)。
ψ=C1ψ1+C2ψ2=C1exp(−iℏ22mEx)+C2exp(iℏ22mEx)
- 由条件 ψ(x=0)=0 得,C1e0+C2e0=C1+C2⟹C1=−C2
ψ(x)=C1ψ1+(−C1)ψ2=C1(ψ1−ψ2)=C1[exp(−iℏ22mEx)−exp(iℏ22mEx)]=−2iC1⎣⎢⎢⎡−2iexp(−iℏ22mEx)−exp(iℏ22mEx)⎦⎥⎥⎤=(−2iC1)sinℏ22mEx=Dsinℏ22mEx
sinxcosx=2ieix−e−ix=2eix+e−ix
- 由条件 ψ(x=a)=0 得,
ψ(x=a)=Dsinℏ22mEa
令 ℏ22mEa=nπ,n=1,2,3,⋯
En=2ma2n2π2ℏ2,ψn(x)=Dnsinanπx
∫0n∣ψn(x)∣2dx∫0n∣Dn∣2sin2anπxdx=1=1=∣Dn∣2∫0nsin2anπxdx=∣Dn∣2∫0n21(1−cosa2nπx)dx=∣Dn∣22a
∣Dn∣=a2 ,取 Dn=a2 ,
最终得到,
ψn(x)=a2sinanπx
# 有限深对称方势阱
核力相互作用势的近似。
![图3-4 图3-4]()
将核力相互作用分开需要 2∼8MeV 的能量,强力是短程力 a=10−13cm( 1 费米),分子的结合能 V0=10eV 。
从物理学角度看,所谓爱情只不过是头脑中的分子作用。
“我爱你有多深(不超过 10−8cm ),我爱你有几分(不多于 10eV )”
![图3-5 图3-5]()
V(x)={0,−2a⩽x⩽2aV0,∣x∣⩾2a
⎩⎪⎪⎪⎨⎪⎪⎪⎧1 区:2 区:3 区:−2mℏ2dx2d2ψ1+V0ψ1=Eψ1−2mℏ2dx2d2ψ2=Eψ2−2mℏ2dx2d2ψ3+V0ψ3=Eψ3
2 区:
ψ2=C1exp(iℏ22mEx)+C2exp(−iℏ22mEx)=C1eikx+C2e−ikx,k=ℏ22mE
1 区:
dx2d2ψ1(x)+ℏ22m⩽0(E−V0)ψ1(x)=0
dx2d2ψ1(x)−ℏ22m(V0−E)ψ1(x)=0
令解 ψ1=eλx,ψ1′=λeλx,ψ1′′=λ2eλx
λ2eλx−ℏ22m(V0−E)eλx=0
λ2=ℏ22m(V0−E)⩾0
λ1=ℏ2m(V0−E)=β,λ2=−ℏ2m(V0−E)=−β(两个线性无关的解)
ψ1(a)(x)=Beβx,ψ1(b)(x)=Ae−βxx→−∞∞发散舍弃
方程整理为:
⎩⎪⎪⎨⎪⎪⎧ψ1=Beβxψ2=C1eikx+C2e−ikxψ3=Ae−βx
对于阱右边界,
⎩⎪⎨⎪⎧ψ2(x=2a)=ψ3(x=2a)ψ2′(x=2a)=ψ3′(x=2a)(波函数在边界连续)
⎩⎪⎨⎪⎧C1eik2a+C2e−ik2a=Ae−β2aC1(ik)eik2a−C2(ik)e−ik2a=−Aβe−β2a(1)(2)
(1)(2):C1eik2a+C2e−ik2aik(C1eik2a−C2e−ik2a)=Ae−β2a−Aβe−β2a=−β
对于阱左边界,
⎩⎪⎨⎪⎧ψ1(x=−2a)=ψ2(x=−2a)ψ1′(x=−2a)=ψ2′(x=−2a)
同理
β=ikC1e−ik2a+C2eik2aC1e−ik2a−C2eik2a
比较两式得,C1=±C2
当 C1=C2 时,
ψ2=C1eikx+C2e−ikx=C1(eikx+e−ikx)
ψ(x)=ψ(−x),为偶宇称
ψ1(−x)=ψ3(x)ψ3(−x)=ψ1(x)}⟹A=B
⎩⎪⎪⎨⎪⎪⎧ψ1=Aeβxψ2=C1(eikx+e−ikx)ψ3=Ae−βx
β=ikC1eik2a+C2e−ik2aC1e−ik2a−C2eik2a=22i⋅ik2eik2a+e−ik2a2ie−ik2a−eik2a=−kcos2ka−sin2ka=ktg2ka
β2a=k2atg2ka
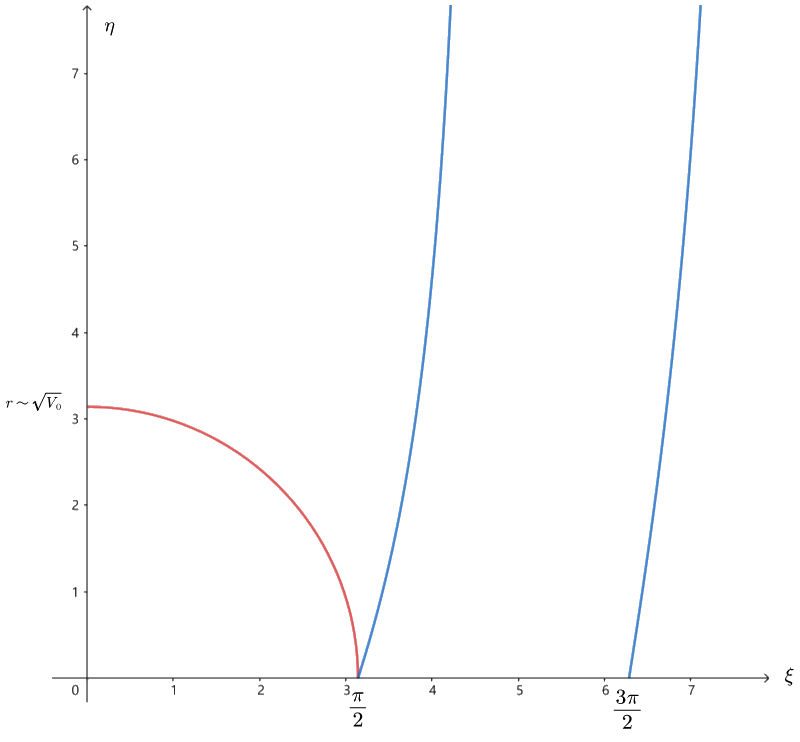
令 ξ=2ka,η=2βa,k=ℏ22mE,β=ℏ22m(V0−E)
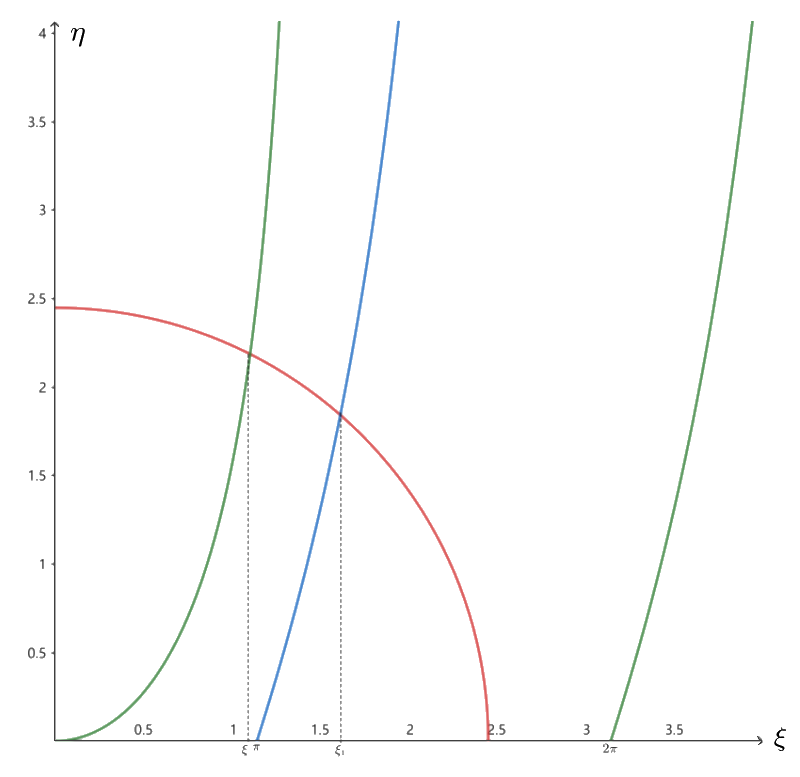
η=ξtgξ,ξ2+η2=(2ka)2+(2βa)2=4a2(k2+β2)=4a2[ℏ22mE+ℏ22m(V0−E)]=4a2ℏ22mV0=2ℏ2ma2V0
![图3-6 图3-6]()
圆 ξ2+η2=2ℏ2ma2V0 与正切函数 η=ξtgξ 交点的 ξ 值为解,阱深有限,圆的半径也有限,则有限个解,有限个束缚态。
⎩⎪⎪⎨⎪⎪⎧ψ1=Aeβxψ2=C1(eikx+e−ikx)=2C1coskx=Dcoskxψ3=Ae−βx
A,D可定出⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧ψ2(x=2a)=ψ3(x=2a)⟹∫−∞∞∣ψ∣2dx=∫−∞−2a∣ψ1∣2dx+∫−2a2a∣ψ2∣2dx+∫2a∞∣ψ3∣2dx=∫−∞−2aA2e2βxdx+∫−2a2aD2cos2kxdx+∫2a∞A2e−2βxdx
当 C1=−C2 时,
−β=ikC1e−ik2a+C2eik2aC1eik2a−C2e−ik2a
β=ikC1e−ik2a+C2eik2aC1e−ik2a−C2eik2a
β=−kctg2ka
2βa=−2kactg2ka⟹⎩⎪⎨⎪⎧η=−ξctgξξ2+η2=2ℏ2mV0a2
![图3-7 图3-7]()
ψ2=C1(eikx−e−ikx)=Dsinkx
ψ1=−Aeβx,ψ3=Ae−βx
{ψ1(−x)=ψ3(x)ψ3(−x)=ψ1(x)⟹A=−B
ψ(x)=Dsinkx,(−2a⩽x⩽2a)
对于方势阱,无论 V0 数值多小,都会存在一个束缚态,其宇称是偶的(仅一维)。
对于处在束缚态的粒子,区域 ∣x∣⩾2a 叫经典禁绝区.dot}(经典力学中,粒子不可能出现在该区域),但在量子力学中,波函数 $\psi (x)\backsim e$ ,β=ℏ22m(V0−E) ,粒子在 x0 点出现几率 ρ(x)dx=∣ψ(x0)∣2dx∽e±2βx0dx 不为零,尽管它随 ∣x∣ 的增大而指数级衰减。这一现象称为隧道穿透(隧道效应)。
![图1-1 弹簧振子 图1-1 弹簧振子]()
经典力学中:
E0=2mP2+21mω02x2=21ω02xmax2⟹xmax2=21mω02E0
![]()
α=ℏmω0,α−1=mω0ℏ=21mω0221ω0ℏ=21mω2E0=xmax=x禁绝
![]()
# 方势垒的反射与穿透(贯穿)
![图3-8 方势垒 图3-8]()
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧1 区:Eψ1=−2mℏ2dx2d2ψ1+V(x)ψ1=−2mℏ2dx2d2ψ12 区:Eψ2=−2mℏ2dx2d2ψ2+V0ψ23 区:Eψ3=−2mℏ2dx2d2ψ3
1 区:
dx2d2ψ1+ℏ22mEψ1=0
k2=ℏ22mE
ψ1(a)=eikx,ψ1(b)=e−ikx
行波有向前的波和反射的波:
ψ1=C1eikx+C2e−ikx=eikx+Re−ikx
2 区:
dx2d2ψ2−ℏ22mE(V0−E)ψ2=0
ψ2(a)=eβx,ψ2(b)=e−βx
ψ2=Aeβx+Be−βx
3 区:
ψ3(a)=eikx,ψ3(b)=e−ikx
ψ1(a)=eikx(无反射波)
ψ入射=eikx
jin=2miℏ[e−ikxdxdeikx−eikxdxde−ikx]=2miℏ[ik−(−ik)]=2miℏ⋅2ik=mℏk
mℏk=mP=v入射(入射波速度,仅是量纲分析,速率在量子力学中无意义)
几率流密度jin=2miℏ[ψ∗∇ψ−ψ∇ψ∗]=2miℏ[ψin∗∇ψin−ψin∇ψin∗],∂t∂ρ+∇⋅j=0
反射系数R=jinj反射=∣R∣2vinvin=∣R∣2透射系数T=jinj透射=∣S∣2vinvin=∣S∣2
x=0 :
{ψ1(x=0)=ψ2(x=0)ψ1′(x=0)=ψ2′(x=0)⟹{1+R=A+Bik(1+R)=β(A−B)(1)(2)
(1)+(2)⎩⎪⎪⎨⎪⎪⎧A=21[(1+βik)+R(1−βik)]B=21[(1−βik)+R(1+βik)]
x=a :
{ψ2(x=a)=ψ3(x=a)ψ2′(x=a)=ψ3′(x=a)⟹{Aeβa+Be−βa=Seikaβ(Aeβa−Be−βa)=ikSeika(3)(4)
(3)+(4)⎩⎪⎪⎨⎪⎪⎧A=2S(1+βik)eika−βaB=2S(1−βik)eika+βa
整理得:
⎩⎪⎪⎨⎪⎪⎧21[(1+βik)+R(1−βik)]=2S(1+βik)eika−βa21[(1−βik)+R(1+βik)]=2S(1−βik)eika+βa(5)(6)
(5)×(1+βik)−(6)×(1−βik) :
(1+βik)2−(1−βik)2=Seika[(1+βik)2eβa−(1−βik)eβa]
双曲余弦函数:chx=2ex+e−x
双曲正弦函数:shx=2ex−e−x
关系:ch2x+sh2x=1
Seika=[−2+2(βk)2]shβa+4i(βk)chβaβ4ik=[1−(βk)2]shβa−2i(βk)chβa−β2ik
T=∣S∣2=(β2−k2)sh2βa+4k2β2ch2βa4k2β2=(β2−k2)2sh2βa+4k2β2−4k2β2sh2βa4k2β2ch2x=1−sh2x=(β2+k2)2sh2βa+4k2β24k2β2=1+4k2β2(β2+k2)2sh2βa1
k2=ℏ22mE,β=ℏ22m(V0−E)
β2+k2=ℏ22mV0
4k2β2(β2+k2)2=4ℏ22mE⋅ℏ22m(V0−E)ℏ44m2V02=ℏ416m2E(V0−E)ℏ44m2V02=4E(V0−E)V02=4V0E(1−V0E)1
T=∣S∣2=⎣⎢⎡1+4V0E(1−V0E)sh2βa⎦⎥⎤−1
R=∣R∣2=(k2+β2)sh2βa+4k2β2(k2+β2)sh2βa
R+T=∣R∣2+∣S∣2=1
当 βa≫1 ,也就是说 ℏ22m(V0−E)a2≫1 时,近似地有 shβa=2eβa−e−βa≅21eβa ,代入 T 后,有
T≅⎣⎢⎡1+4V0E(1−V0E)1⋅41e2βa⎦⎥⎤−1=⎣⎢⎡4V0E(1−V0E)1⋅41e2βa⎦⎥⎤−1=V0216E(V0−E)e−2βa=V0216E(V0−E)exp(−ℏ2a2m(V0−E))
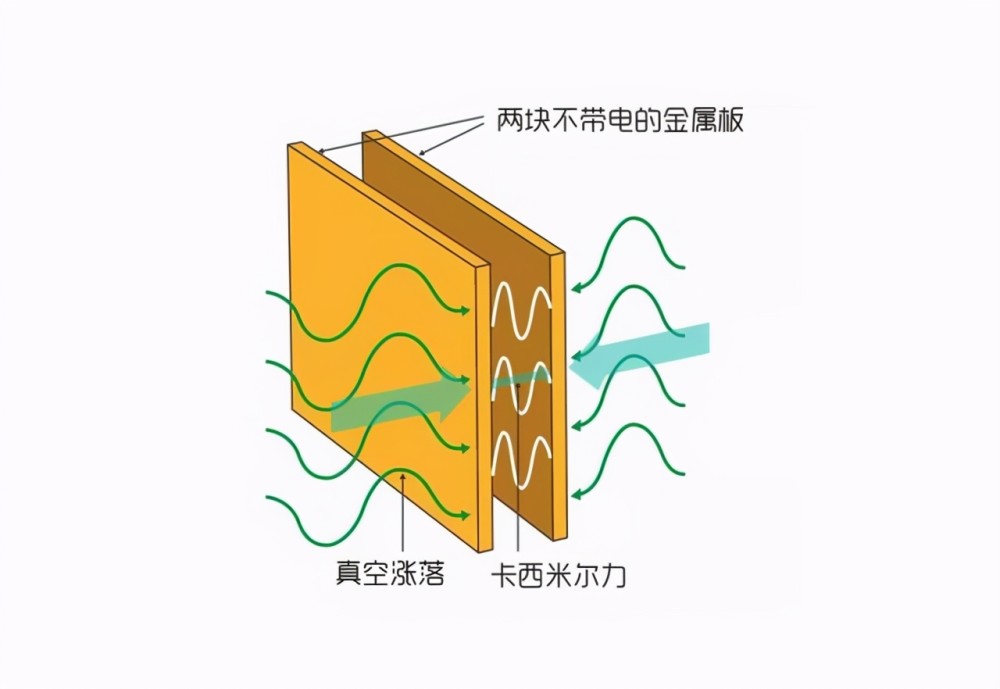
卡西米尔 1948 年提出,“真空之力”
![卡西米尔效应 卡西米尔效应]()
两块中性金属板之间充满电磁场形成的驻波。
(非严格证明)
E总=21ℏω0(1)+21ℏω0(2)+⋯=∞
左移金属板,ω 改变
E~总=21ℏω~0(1)+21ℏω~0(2)+⋯=∞
E~总−E总=ΔE
卡西米尔力 F 为负值,也就是向右的吸引力。
范德华力(范德瓦尔斯力,又称分子间相互作用力)
两个中性原子(或分子):
![]()
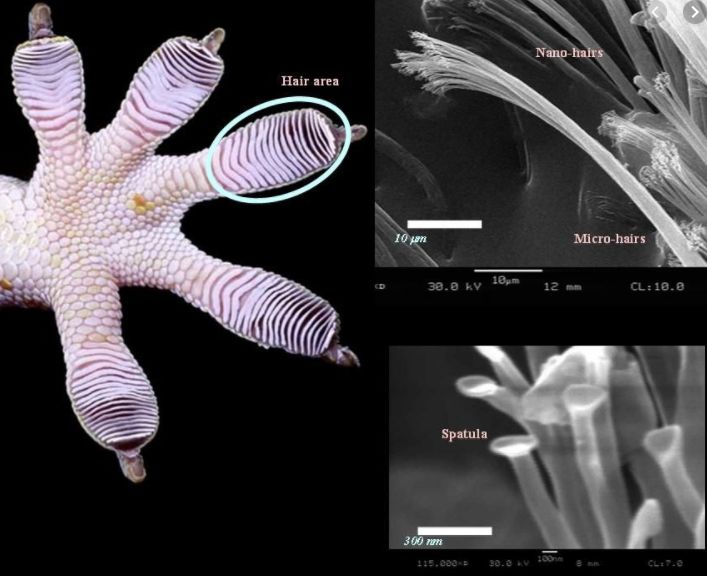
伦敦指出,两个原子在不断振动,会有一个瞬时的偶极矩。范德华力是卡西米尔效应在分子尺度的宏观表现,卡西米尔效应是范德华力的微观效应。常见是蜘蛛、壁虎爬墙的力。
![壁虎 壁虎]()
![卢卡斯 卢卡斯]()
# 参考资料


![图3-6 图3-6]()
![图3-7 图3-7]()