理论是什么?客观世界的规律在人脑内的反应,是一个图像,与真实所见的图像相比,永远存在失真。三维图像映射到人眼的视网膜上,二维图像永远只是三维图像的近似。如果从这个图像出发,进行逻辑的推理,得到一些结论(预言),再去做实验进行验证,若实验结果与预言非常接近,这种情况下,我们就能说图像是足够完备的。
# 经典物理无法解释的四个问题
#黑 体辐射实验
黑体就是一个将射在其上的电磁波能量完全吸收的物体。
![黑体模型 黑体模型]()
如一个空腔。以电磁波形式辐射自身能量,最终达到热力学平衡。
用 Eν 表示辐射能量密度,Eνdν 表示在单位体积内、频率在 (ν,ν+dν) 之间的辐射能量。
1896 年,W. Wien 从热力学普适理论出发,结合实验数据,得出半经验公式:
Eνdν=C1ν3eT−C2νdν
C1 ,C2 为经验参数。
短波段符合很好,长波极限不好
J.W. Rayleigh(1900 年)和 J.H. Jeans(1905 年)提出如下公式:
Eνdν=c38πkTν2dν≅Tν2dν
长波极限符合很好,短波符合不好(紫外灾难)。
Rayleigh-Jeans 公式推导
在一有限立方体内,电磁波为驻波,其一般形式为
E=E0sinLn1πxsinLn2πysinLn3πz,ni=0,±1,±2,⋯
ni 称为允许模式。每个模式所占据的相空间体积为 Δk=(Lπ)3 。对于电磁波,有 ω=c∣k∣ 。因此空腔内的电磁波模式密度为
g(ω)dω=k∑δ(ω−c∣k∣)dω=Sk=cωdω≅ω2dω≅ν2dν
根据统计力学中的能量均分定理,电磁波每一个允许模式的平均能量为 21kT
Eνdν∽21kTg(ω)dω≅kTν2dν
# 光电效应
1888 年,H.Hertz 发现光电效应。当一束紫外光照射到金属表面时,会有电荷逸出。
1896 年,J.J. Thomson 发现电子。
光电效应特点:
- 对于特定的金属材料做成的电极,存在一个确定的临界频率 ν0 ,当照射光的频率 ν⩾ν0 时,无论光强多大,不会观察到有电子被激发出来;
- 每个出射电子的能量仅与照射光的频率 ν 有关;
- 当入射光的频率 ν>ν0 时,无论光束多么微弱,都会产生光电效应。
# 原子的线状光谱及其规律
1885 年,Balmmer 发现氢原子的可见光谱是分立的:
ν~=λ1=R(221−n21),n=3,4,⋯
ν~ 为波数,即波长的倒数,Rydberg 常数 R=109,677.581cm−1
1903 年,W. Ritz 归纳提出原子发出的光谱线的波数 ν~ 总能写成
ν~nm=T(n)−T(m),n,m为正整数。
# 原子的稳定性
1895 年,Röntgen 发现了 X 射线,Bequerrel 发现了铀盐的天然放射性。
1898 年,居里夫妇发现了镭。
1904 年,Thomson 提出 “葡萄干面包模型”(中文语境也就是 “枣糕模型” ):正电荷均匀分布在原子中,而电子则在其中做某种有规律的排序。
1911 年,Rutherford 分析了用 α 粒子轰击原子,发现无法解释观测到的大角度散射现象。他提出:原子中的正电荷部分集中在一个很小的区域中( <10−12cm ),同时原子质量的主要部分也集中在这一区域,形成原子核,而电子则围绕着原子核旋转。
Rutherford 原子模型缺陷:按照经典电动力学,电子在原子核外做加速运动,能量会以电磁波形式向外不断辐射出去,最终电子会掉入原子核,这与现实中原子是稳定的不相符。
# Planck-Einstein 的光量子论
1900 年 10 月 19 日,Planck 提出能量子的概念,发表黑体辐射公式:
Eνdν=eT−C2νC1ν3dν
1900 年 12 月 4 日,量子力学始端。
1905 年,Einstein 提出光量子概念,爱因斯坦方程:
21mv2=hν−A
1923 年,Compton 散射实验证明了光的粒子性。
# Bohr 量子论
1911 年 Bohr 获得博士学位,9 月赴剑桥,在 Thomson 领导的 Cavendish 实验室短暂停留( Thomson 忙于行政工作,没空管 Bohr 发给他的论文),期间恰巧遇到来学术交流的 Rutherford(机遇来的总是莫名其妙),二人结缘后,Bohr 赴位于 Manchester 的由 Rutherford 领导的实验室,交给他的课题就是 “如何解释原子的稳定性” 。
1912 年:
- 原子只能够稳定地存在于与分立能量对应的一系列状态,这些态称为定态。因此,体系能量的任何改变,包括吸收和发射电磁波,都必须在两个定态之间以跳迁(跃迁)的方式进行;
- 在两个定态之间跳迁时,原子吸收或发射的电磁波频率是唯一的,其值为 hν1,2=E1−E2 ,E1 和 E2 是相应的定态能量;
- 对应原理:当某个定态的量子数 n 非常大时,这个态所对应的物理量应该接近经典物理给出的数值。在 Bohr 的哲学观念里,世界是统一的,在微观和宏观之间不存在人为设定的边界。
利用玻尔理论推导氢原子能级
![电子的经典轨道 电子的经典轨道]()
电子受原子核吸引处于束缚态,电子的库伦势:
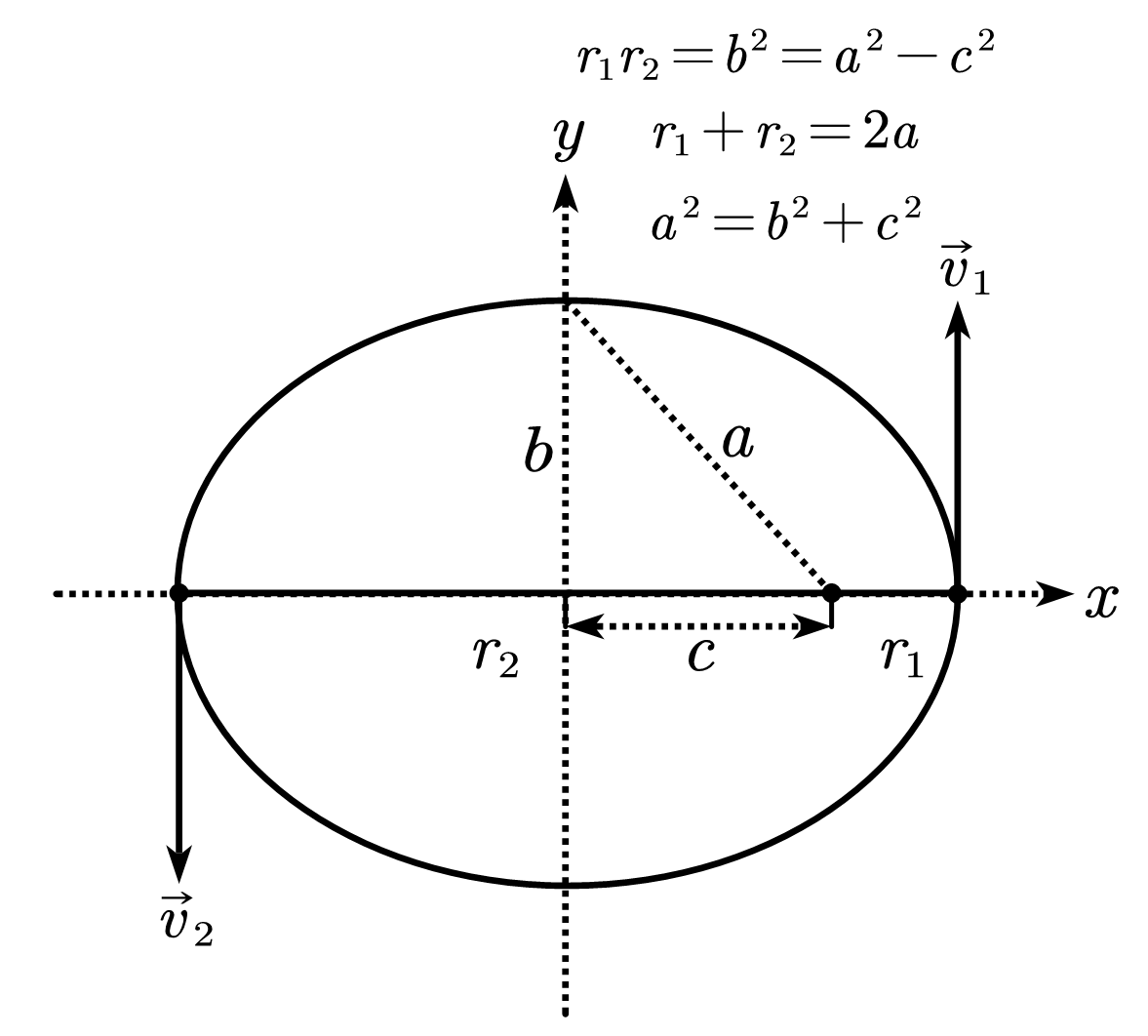
V(r)=−re2=−rK
E=−2aK,T2=K4π2ma3
由机械能守恒得,
21mv12−r1K=21mv22−r2K(1)
由角动量守恒得,
mr1v1=L=mr2v2(2)
将 v1=mr1L ,v2=mr2L 带入 (1) 得:
2mr12L2−r1K=E,2mr22L2−r2K=E
分别乘上 r12 和 r22 ,
r12E=2mL2−Kr1,r22E=2mL2−Kr2
左式减右式得,
(r12−r22)E(r1+r2)EE=K(r2−r1)=−K=−2aK(3)
左式加右式得,
(r12+r22)EL2=mL2−(r1+r2)K=[(r12+r22)E+(r1+r2)K]m=[(r12+r22)E+2r1r2E−2r1r2E+2aK]m=[(r1+r2)2E−2r1r2E+2aK]m=[4a2E−2(a2−c2)E+2aK]m=(4a2E−2b2E+2aK)m=−2mb2E(4)
第二次将(3)代入(4)中,
L2=−2mb2(−2aK)=amKb2⇒L=amKb
![曲边三角形微元 曲边三角形微元]()
L=∣r×P∣=rmvsinθ=Δt→0limrmΔtΔSsinπ−α=Δt→0limmΔtΔSrsinα=Δt→0lim2mΔtΔS
∫0TLdt=∫0T2mdtdSdt⇒L∫0Tdt=2m∫0TdS⇒LT=2m×椭圆面积=2mπab
2mπaKmbab=T=L2mπab
T2=K4π2ma3=K4π2m(2E−K)2,(E=−∣E∣)=2∣E∣3π2mK2
电子绕原子核运动的频率为 ν=T1=πK1m2∣E∣23=πK1m2(−E)23 。
假定氢原子中电子的状态是分立的,故可以用一个整数 n 加以标记,称为该状态的量子数:
ν=T1=πK1m2∣E∣23,n为主量子数
Bohr 对应原理要求 n→∞ 时,对应状态的行为可以用经典物理来描述。
现在求解 E(n) 与 n 的关系
Bohr 假设每一个量子态的能量可以写作
E(n)=hν(n)f(n)
ν(n) 为对应于 E(n) 的电子经典轨道频率,f(n) 是一个无量纲函数。
当 n→∞ 时,
hνn,n−1=E(n)−E(n−1)≅E′(n)Δn=E′(n)
n→∞,dndE(n)≅E′(n)
E′(n) 为能量函数的导数。
为求解 E′(n) ,先求解 f′(n) :
f′(n)=dndf(n)=dnd[hνnE(n)]=hνnE′(n)+hE(n)dnd(νn1)=hνnE′(n)−hν2(n)E(n)dE(n)dν(n)dndE(n)=hνnE′(n)[1−E(n)dE(n)dlnν(n)]
解得
E′(n)=hν(n)f′(n)[1−E(n)dE(n)dlnν(n)]−1
根据对应原理,电磁波的辐射频率 νn,n−1 在量子数 n 很大时接近于加速电子辐射的经典频率,即电子绕原子核运动的轨道频率 ν(n) ,
hν(n)≅hνn,n−1≅E′(n)=hν(n)f′(n)[1−E(n)dE(n)dlnν(n)]−1
利用 ν(n)=T(n)1=πK1m2∣E(n)∣23=πK1m2[−E(n)]23 得
f′(n)=1−E(n)dE(n)dlnν(n)=1−23=−21
因此,当 n 很大时,我们有 f(n)=−21n+D ,D 为常数。
Bohr 假设当 n 较小时也成立,即 E(n)=hν(n)f(n)=hν(n)(−21n+D)
将 ν(n)=πK1m2∣E(n)∣23 代入得
E(n)=−∣E(n)∣=hν(n)f(n)=πKhm2∣E(n)∣23(−21n+D)
即 ∣E(n)∣21=2h(−21n+D)πKm
两边平方得
E(n)=−∣E(n)∣=−2h2(−21n+D)2π2K2m
在友人 Hanssen 督促下,考虑氢原子的光谱问题。他令 D=0 ,
E(n)=−n2h22π2K2m=−n2h22π2e4m
利用 hνn,m=E(n)−E(m) ,计算光谱线 hν2,n,n=3,4,⋯
hν2,n=E(2)−E(n)=−22h22π2e4m+n2h22π2e4m=−h22π2e4m(221−n21),n=3,4,⋯
与氢原子的 Balmmer 系谱
ν~=λ1=R(221−n21),n=3,4,⋯
一致,其中根据 Bohr 理论 R=−h22π2e4m 。
# Bohr-Sommerfeld 量子化条件
L=∮pdq=(n+21h)
p 为广义动量,q 为广义坐标,n 为主量子数。对于谐振子,∮pdq=nh
# Heisenberg 和 Dirac 的矩阵力学
Bohr 理论只适用于氢原子,对复杂原子不适用,理论研究陷入停滞。
1925 年夏季,6 月 7 日,Heisenberg 因为 “枯草热” 前往 Helgoland 小岛休假,并重新思考了 Bohr 理论。
以下是从 Dirac 后来的概括中获取到的信息:
- 物理理论应建立在与实验观测量紧密联系的物理量上,而 “轨道” 无法观察到;
- 舍弃 “轨道” 概念,改用 “状态” 代替;
- 可观测物理量仅与两个状态相联系,物理量写成矩阵形式:
⎝⎛××××××⋯⋯⋯⎠⎞每一行与一个态相关,每一列与另一个态相关。
把力学量写成矩阵形式。人们所建立的理论以可观测量为基础,而可观测量是力学量矩阵的矩阵元,每个矩阵元与两个态相关。
对于氢原子,每个能级有一个量子数 n 。
电子 x 坐标写成:
x^=⎝⎛x11x21⋯x12x22⋯⋯⋯⋯x1nx2n⋯⋯⋯⋯⎠⎞
相应动量 P^x 为:
P^x=⎝⎛P11P21⋯P12P22⋯⋯⋯⋯P1nP2n⋯⋯⋯⋯⎠⎞
xmn 和 Pmn 称为力学量 x^ 和 P^x 在 m 态和 n 态之间的跳迁矩阵元。
对于两个矩阵,相乘时左右位置对换,其值一般不相等,及 A^B^=B^A^ 。(线性代数中叫不可交换,量子力学中叫不对易,硬说区别就是力学量矩阵包含着物理意义)
对易子[x^,P^x]≡x^P^x−P^xx^=0
关于对易子 [x^,P^x] 等于什么,由 Dirac 在 1925 年夏天加以解决。
Dirac 回忆了分析力学中的 Poisson 括号:
{u,v}≡i∑(∂qi∂u∂pi∂v−∂pi∂u∂qi∂v)
u 和 v 是任意两个广义坐标与广义动量( q1,q2,⋯,qN,p1,p2,⋯,pN )的函数。
- {u,v}=−{v,u}
- {u,C}=0,C为常数
- {u1+u2,v}={u1,v}+{u2,v}
- {u,v1+v2}={u,v1}+{u,v2}
- {u1u2,v}={u1,v}u2+u1{u2,v}
- {u,v1v2}={u,v1}v2+v1{u,v2}
- {u,{v,ω}}+{v,{ω,u}}+{ω,{u,v}}=0
对易子满足以上 Poisson 括号的关系式。
此时用矩阵 u^,v^ 代替经典力学量 u,v 。
Dirac 提出,量子力学的对易子 [u^,v^] 正比于经典力学中的 Poisson 括号 {u,v} :
[u^,v^]=D{u,v}
注:只是计算形式上的 “等于”
[x^,P^x]=D{x,Px}=D(∂x∂x∂Px∂Px+∂y∂x∂Py∂Px+∂z∂x∂Pz∂Px−∂Px∂x∂x∂Px−∂Py∂x∂y∂Px−∂Pz∂x∂z∂Px)=D∂x∂x∂Px∂Px=D×1=D
同理 [y^,P^y]=[z^,P^z]=D
以及
[x^,P^y]=[x^,P^z]=[y^,P^x]=[y^,P^z]=[z^,P^x]=[z^,P^y]=0
[x^,y^]=[x^,z^]=[y^,z^]=[P^x,P^y]=[P^x,P^z]=[P^y,P^z]=0
“不共轭就对易” : x 和 Px 是共轭的,这里指脚标是一样的,都是 x ;x 和 Py 、Pz 是不共轭的;对易指位置对换后差值为 0 ,换位跟没换一样。
以上这些对易关系称为量子力学的基本关系式,可以证明 D=iℏ 。
量纲分析:[ℏ]=[E][T]=LMT−1
由 Pauli 验证了以下对易关系:
- [r^,P^2]=2DP^,[r^,(P^)n]=inℏ(P^)n−1=iℏ∂P^∂(P^)n
- [P^⋅r^,P^2]=2DP^
- r^⋅P^−P^⋅r^=3D
- [r^,P^⋅r^]=[r^,r^⋅P^]=Dr^
- [P^,r^1]=Dr^3r^
- [P^,r^31]=3Dr^5r^
- [P^⋅r^,r^1]=Dr^1
- [P^2,r^1]=D[r^31(r^⋅P^)+(P^⋅r^)r^31]
- [(P^⋅r^)P^,r^1]=D[r^1P^+(P^⋅r^)r^3r^]
- P^×L^=P^2r^+DP^−(P^×r^)P^,其中L^=r^×P^为该粒子的角动量算符。
补充:[A^,B^m]=mB^m−1[A^,B^]
验证 2、5、10
(2)
[P^⋅r^,P^2]=[P^xx^+P^yy^+P^zz^,P^2+P^2+P^2]=[P^xx^,P^2+P^2+P^2]+[P^yy^,P^2+P^2+P^2]+[P^zz^,P^2+P^2+P^2]=[P^xx^,P^x2]+[P^xx^,P^y2]+[P^xx^,P^z2]+[P^yy^,P^x2]+[P^yy^,P^y2]+[P^yy^,P^z2]+[P^zz^,P^x2]+[P^zz^,P^y2]+[P^zz^,P^z2]=[P^xx^,P^x2]+[P^yy^,P^y2]+[P^zz^,P^z2]=2D(P^x2+P^y2+P^z2)=2DP^
利用 {u1u2,v}={u1,v}u2+u1{u2,v} 和 {u,v1v2}={u,v1}v2+v1{u,v2}
[P^xx^,P^y2]=[P^x,P^y2]x^+P^x[x^,P^y2]=P^y[P^x,P^y]x^+P^x[x^,P^y]P^y=0
[P^xx^,P^x2]=[P^x,P^x2]x^+P^x[x^,P^x2]=P^x[x^,P^x2]=P^x{[x^,P^x]P^x+P^x[x^,P^x]}=P^x[DP^x+DP^x]=2DP^x2
(5)
\begin{aligned} \left[\hat{\vec{P}}, \frac{1}{\hat{r}}\right]&=\left[\hat{P}_{x}\vec{i}+\hat{P}_{y}\vec{j}+\hat{P}_{z}\vec{k}, \frac{1}{\hat{r}}\right]\\ &=\left[\hat{P}_{x}, \frac{1}{\hat{r}}\right]\vec{i}+\left[\hat{P}_{y}, \frac{1}{\hat{r}}\right]\vec{j}+\left[\hat{P}_{z}, \frac{1}{\hat{r}}\right]\vec{k}\\ &=D\frac{\hat{x}}{\hat{r}^{3}}+D\frac{\hat{y}}{\hat{r}^{3}}\vec{j}+D\frac{\hat{z}}{\hat{r}^{3}}\vec{k}\\ &=D\frac{\hat{x}\vec{i}+\hat{y}\vec{j}+\\hat{z}\vec{k}}{\hat{r}^{3}}\\ &=D\frac{\hat{\vec{r}}}{\hat{r}^{3}} \end{aligned}
a×(b×c)=b⋅(a⋅c)−(a⋅b)c
隔空点乘:P^r^P^=P^xr^P^x+P^yr^P^y+P^zr^P^z
目的:保持顺序,即 r在 P的右边。
[P^x,r^1]=D{Px,r1}=D{∂x∂Px∂Px∂r1+∂y∂Px∂Py∂r1+∂z∂Px∂Pz∂r1−∂Px∂Px∂x∂r1−∂Py∂Px∂y∂r1−∂Pz∂Px∂z∂r1}=−D∂Px∂Px∂x∂r1=−D∂x∂x2+y2+z21=−D(−21)(x2+y2+z2)232x=Dr^3x^
(10)
P^×L^=P^×(r^×P^)=r^⋅(P^⋅P^)−(P^⋅r^)⋅P^=P^⋅r^⋅P^−(P^⋅r^)P^=P^xr^P^z+P^yr^P^y+P^zr^P^z−(P^⋅r^)⋅P^=(r^P^x2−DP^xi)+(r^P^y2−DP^yj)+(r^P^z2−DP^zk)−(P^⋅r^)⋅P^=r^P^2−DP^−(P^⋅r^)⋅p^
P^xr^P^x=P^x(x^i+y^j+z^k)P^x=P^xx^P^xi+P^xy^P^xj+P^xz^P^xk=P^xx^P^xi+y^P^xP^xj+z^P^xP^xk=x^P^xP^xi−DP^xi+y^P^xP^xj+z^P^xP^xk=r^P^x2−DP^xi
[y^,P^x][x^,P^]=y^P^x−P^xy^=0⇒y^P^x=P^xy^=x^P^x−P^xx^=0⇒x^P^x−D=Px^x^
Heisenberg 论文一作,Born 和 Jordan 论文二作,最后三个人三作弄出矩阵力学。
Pauli 利用矩阵力学求解氢原子的能级
在向心力场中,除了机械能守恒、角动量守恒,还有拉普拉斯 -龙格- 楞次向量守恒。
经典力学形式:
A=rr−P×L
量子力学形式:
A^=r^r^−21(P×L−L×P)
A是个守恒量:dtdA=0
满足
[L^i,A^j][A^i,A^j]=DϵijkA^k=Dϵijkme4(−2E)L^k
其中 E=2mP2−re2,L^=r^×P^
i=x,y,zj=x,y,z
反对称记号 ϵijk ,i,j,k 分别对应 1,2,3 。当 ijk 为偶排列时,记号为 + 号;当 ijk 为奇排列时,记号为 − 号。
引入记号 u^i=−2Eme4A^i
改写为
[L^i,u^j][u^i,u^j]=Dϵijku^k=DϵijkL^k
同时角动量算符满足 [L^i,L^j]=DϵijkL^k
引入新矩阵 j^1≡21(L^+u^)
可证明其满足 [j^1i,j^1j]=Dϵijkj^1k
其卡西米尔算符 j^12=j^1x2+j^1y2+j^1z2 的取值为
−j1(j1+1)D2,j1=0,21,1,23,⋯
李群的生成元
另一方面,可验证 L^⋅u^=u^⋅L^=0 及 L^2+u^2=D2−2Eme4
因此
−j1(j1+1)D2=j^12=41(L^+u^)2=41(L^2+u^2+L^⋅u^+u^⋅L^=41(D2−2Eme4=4D2−8Eme4
由此得 −4j1(j1+1)D2=D2−2Eme4 或者 (−4j12−4j1−1)D2=−(2j1+1)2D2=−2Eme4
解得
E=2(2j1+1)2D2me4
现在令 2j1+1=n ,当 j1 取 0,21,1,23,2,⋯ 时,n 的取值为 1,2,3,⋯
因此氢原子的能级为
E(n)=2n2D2me4
将上式与 Bohr 所得氢原子能级比较
E(n)=−n2h22π2me4
比较得 D2=−(2πh)2=−ℏ2 或者 D=iℏ
最后得到量子力学的基本方程式 [x^,P^x]=iℏ
# Dirac 正则量子化规则
对于一个给定的物理体系,其量子力学形式可以如下建立
- 先找到该体系的经典广义坐标 q1,q2,⋯,qN ,并写出拉格朗日量
L(q1,q2,⋯,qN,q˙1,q˙2,⋯,q˙N)=T−V
一维谐振子的拉式量 L=21mv2−21kx2
验证拉式量是否正确
将 L 代入拉格朗日方程
dtd∂q˙i∂L=∂qi∂L
看是否能够得到牛顿方程
mdt2d2r=F
计算广义动量
pi≡∂q˙i∂L
q˙i 为广义速度,是 qi 的一阶导数。
写出哈密顿量
H≡i=1∑Npiq˙i−L=H(q1,q2,⋯,qN,p1,p2,⋯,pN)
量子化:将力学量 (p1,p2,⋯,pN) 和 (q1,q2,⋯,qN) 换成相应的矩阵 (p^1,p^2,⋯,p^N) 和 (q^1,q^2,⋯,q^N) ,并要求
[q^i,p^j]=iℏδij,[q^i,q^j]=[p^i,p^j]=0
克罗内克记号δij={1(i=j)0(i=j) ,狄拉克 δ 函数是克罗内克记号的推广。
由此得到的哈密顿量矩阵 H^(q^1,q^2,⋯,q^N,p^1,p^2,⋯,p^N) 就决定了该体系的动力学行为。
# De Broglie 的物质波和 Schrödinger 的波动力学
1924 年,De Broglie 从 Planck 和 Einstein 的光量子理论出发,提出质量 m=0 的粒子具有波粒二象性。
于是他在自己的博士论文里加入,
粒子物质波具有:ψ(r,t)=ψ0exp(ik⋅r−iωt)
能量关系:E=hν=2πh2πν=ℏω动量关系:P=λhk0=2πhλ2πk0=ℏk
这将粒子能量 E 、动量 P与频率 ν 、波矢 k联系起来。
![图5-1 图5-1]()
氢原子中作稳定圆轨道的电子波形应是驻波波形,波绕原子传播一周光滑衔接起来,因此圆轨道周长应是波长的整数倍,即:
2πR=nλ,n=1,2,3,⋯
利用 De Broglie 关系 P=λh 有
L=RP=R(n2πR)h=2πnh=nℏ
即 Bohr 的角动量量子化条件。De Broglie 用了很简单的原理推出 Bohr 很复杂的东西。
从 De Broglie 关系,Schrödinger 提出如下对应关系:
E⇔iℏ∂t∂,2mP2⇔−2mℏ2∇2
对于一个自由粒子,有关系 E=2mP2 ,又考虑到自由粒子的 De Broglie 波可写作
ψ(r,t)=ψ0exp(ik⋅r−iωt)
则有
Eψ(r,t)Eψ0exp(ik⋅r−iωt)=2mP2ψ(r,t)=2mP2ψ0exp(ik⋅r−iωt)
将 E⇔iℏ∂t∂,2mP2⇔−2mℏ2∇2 代入得 (E=hω,P=ℏk)
hωψ0exp(ik⋅r−iωt)=2m(ℏk)2ψ0exp(ik⋅r−iωt)=2mℏ2k2ψ0exp(ik⋅r−iωt)
iℏ∂t∂ψ(r,t)=ℏ−i1∂t∂ψ0exp(ik⋅r−iωt)=2mℏ2k2ψ0exp(ik⋅r−iωt)=−2mℏ2∇2ψ(r,t)
由此,他推导出了自由粒子的 Schrödinger 方程:
iℏ∂t∂ψ(r,t)=−2mℏ2∇2ψ(r,t)
自由粒子的 De Broglie 行波 ψ(r,t)=ψ0exp(ik⋅r−iωt)
与通常的热扩散方程 C∂t∂ψ(r,t)=−D∇2ψ(r,t) 最大的区别在于算符 ∂t∂ 前的系数为纯虚数 iℏ 。
对于有外场的 Schrödinger 方程:
iℏ∂t∂ψ(r,t)=−2mℏ2∇2ψ(r,t)+V(r)ψ(r,t)
利用 Schrödinger 方程求解氢原子的能级
对于球坐标:
r=xi+yj+zk
⎩⎪⎪⎨⎪⎪⎧0⩽r<∞,0⩽θ<π,0⩽φ<2π,z=rcosθtanφ=xyr2=x2+y2+z2
∇2=r21∂r∂r2∂r∂+r21(sinθ1∂θ∂sinθ∂θ∂+sin2θ1∂φ2∂2)
对于氢原子,iℏ∂t∂ψ(r,t)=−2mℏ2∇2ψ(r,t)−re2ψ(r,t)
利用分离变量法求解此方程,令 ψ(r,t)ϕ(r)e−iωt , ω 待定。
方程左边:
iℏ∂t∂ϕ(r)e−iωt=iℏϕ(r)∂t∂e−iωt=iℏ(−iω)ϕ(r)e−iωt=ℏωϕ(r)e−iωt
方程右边:
−2mℏ2∇2ϕ(r)e−iωt−re2ϕ(r)e−iωt
整理(约去 e−iωt ):
ℏωϕ(r)=−2mℏ2∇2ϕ(r)−re2ϕ(r)
求解定态方程(与时间无关),求解本征值问题,代入球坐标下的拉普拉斯算符 ∇2 ,
Eϕ(r)=−2mℏ2[r21∂r∂r2∂r∂+r21(sinθ1∂θ∂sinθ∂θ∂+sin2θ1∂φ2∂2)]ϕ(r)−re2ϕ(r)(1)
令 ϕ(r)=ϕ(r,θ,φ)=R(r)YLM(θ,φ) 代入(1)得
Eϕ(r)=ER(r)YLM(θ,φ)=−2mℏ2[r21∂r∂r2∂r∂R(r)YLM(θ,φ)+sinθ1∂θ∂sinθ∂θ∂YLM(θ,φ)+sin2θ1∂φ2∂2YLM(θ,φ)R(r)]−re2R(r)YLM(θ,φ)=−2mℏ2r21drdr2drdR(r)YLM(θ,φ)−2mℏ2[−L(L+1)YLM(θ,φ)R(r)]−re2R(r)YLM(θ,φ)
ER(r)=−2mℏ2r21drdr2drdR(r)+2mr2ℏ2L(L+1)R(r)−re2R(r)
引入 R(r)=rχL(r)
r21drdr2drdR(r)=r21drdr2[rχL(r)]′=r21drdr2[rχL′(r)−r2χL(r)]=r21drd[rχL′(r)−χL(r)]=r21rχL′(r)=r1χL′(r)
ER(r)ErχL(r)EχL(r)=−2mℏ2r21drdr2drdRL(r)+2mr2ℏ2L(L+1)RL(r)−re2RL(r)=−2mℏ2r1χL′′(r)+2mr2ℏ2L(L+1)rχL(r)−re2rχL(r)=−2mℏ2χL′′(r)+2mr2ℏ2L(L+1)χL(r)−re2χL(r)
χL′′(r)+[ℏ22m(E+re2)−r2L(L+1)]χL(r)=0福克斯积分方程
球谐函数:
YLM(θ,φ)=(−1)M4π(L+M)!(2L+1)(L−M)PLM(cosθ)eiMφ
勒让德函数:
PL(x)=2LL!1dx2d(x2−1)L,(−1⩽x⩽1)
连带勒让德函数:
PLM(x)PL−M(x)=2LL!1(L−x2)2MdxL+MdL+M(x2−1)L=(1−x2)2MdxMdMPL(x)(M⩾0)=(−1)M(L+M)!(L−M)!PLM(x)
[sinθ1∂θ∂sinθ∂θ∂+sin2θ1∂φ2∂2]YLM(θ,φ)≡sinθ1∂θ∂sinθ∂θ∂YLM(θ,φ)+sin2θ1∂φ2∂2YLM(θ,φ)=−L(L+1)YLM(θ,φ)
作奇异点分析,列出所有奇异点:
- r→0 是一个奇异点
- r→∞ 永远是一个可能的奇异点
χL′′(r)+ℏ22mEχL(r)≅0,E是待定常数
dr2d2χL(r)+ℏ22mEχL(r)≅0,渐近方程
渐近解为 χL(1)(r)=exp(−ℏ2−2mEr),χL(2)(r)=exp(ℏ2−2mEr)
χL′′(r)+[ℏ22mre2−r2L(L+1)]χL(r)=0
当 r→0 时,
χL′′(r)+[ℏ22mre2−r2L(L+1)]χL(r)≅0
r2L(L+1)/ℏ2r22me2∼r1r→0∞
χL′′(r)+r2L(L+1)χL(r)≅0
渐近解:
χL(1)(r)=rL+1,χL(2)(r)=r−L(发散,舍弃)
所以χL(1)(r)=rL+1
令χL(r)=χL(1)(r)χL(a)(r)uL(r) 代入χL′′(r)+[r22m(E+r2e2)−r2L(L+1)]χL(r)=0
uL′′(r)rL+1+[2(L+1)rL−2rL+1ℏ2−2mE]uL′(r)−[L(L+1)rLℏ2−2mE−ℏ22me2rL]uL′(r)=0
两边同除 rL
rdr2d2uL(r)+[2(L+1)−2rℏ2−2mE]drduL(r)−[L(L+1)ℏ2−2mE−ℏ22me2]drduL(r)=0
令 2ℏ2−2mEr=ξ ,
drduL=dξduLdrdξ=2ℏ2−2mEdξduL,dr2d2uL=(2ℏ2−2mE)2dξ2d2uL
ξdξ2d2uL+[2(L+1)−ξ]dξduL−2ℏ2−2mE[2(L+1)ℏ2−2mE−ℏ22me2]uL=0
合流超几何微分方程:
ξdξ2d2u(ξ)+(γ−ξ)dξdu(ξ)−αu(ξ)=0
( γ,α 为常数)
ξ 在 0 处的解析解:
F(α,γ,ξ)=1+γαξ+2!1γ(γ+1)α(α+1)ξ2+3!1γ(γ+1)(γ+2)α(α+1)(α+2)ξ3+⋯
令 γ=2(L+1),α=2ℏ2−2mE2(L+1)ℏ2−2mE−ℏ22me2=(L+1)−ℏ2ℏ2−2mEme2
当 ξ=0 时,解析解为:
F(α,γ,ξ)=1+γαξ+γ(γ+1)2!α(α+1)ξ2+γ(γ+1)(γ+2)3!α(α+1)(α+2)ξ3
当 ξ→∞ 时,F(α,γ,ξ)∼eξ=exp(2ℏ2−2mEr) ,
这使得波函数 χL(r) 在 r→∞ 时,渐近成为
χL(r)=χL(1)(r)χL(α)(r)uL(r)∼rL+1exp(−ℏ2−2mEr)exp(2ℏ2−2mEr)=rL+1exp(−ℏ22mEr)
它是发散的,为了摆脱波函数在 ξ∼r→∞ 时的发散问题,需要将合流超几何级数 F(α,γ,ξ) 加以截断。即令 α=−nr ,
对某一个正整数 nr 成立。从这一条件,我们得到
α=(L+1)−ℏ2ℏ2−2mEme2=−nr
解此方程,ℏ2ℏ2−2mEme2=L+1+nr≡n 或是 −2mE=nℏme2
由此解得氢原子的能级
En=−2m1n2ℏ2m2e4=−2n2ℏ2me4=−n2ℏ22π2me4
与 Bohr 理论给出的完全一样。相应的波函数则为
ψ(r,t)≅r1e−2ξrL+1F(−nr,2(L+1),ξ)YLM(θ,φ)exp(−ℏiEt),ξ=2−ℏ22mEr
A^u=⎝⎜⎜⎜⎛a11a21⋯an1a12a22⋯an2⋯⋯⋯⋯a1na2n⋯ann⎠⎟⎟⎟⎞⎝⎜⎜⎜⎜⎛u1u2⋮un⎠⎟⎟⎟⎟⎞=C⎝⎜⎜⎜⎜⎛u1u2⋮un⎠⎟⎟⎟⎟⎞=Cu
C 为本征值,u=⎝⎜⎜⎜⎜⎛u1u2⋮un⎠⎟⎟⎟⎟⎞ 为本征向量。
∫−11PL(x)PL′(x)dx=2L+12δLL′,(−1⩽x⩽1)
对全空间积分:
∫0∞∫0π∫02πr2drsinθdθdφYL′M′∗(θ,φ)YLM(θ,φ)=δL′LδM′M
从求解氢原子能级的过程可以看出,虐猫狂魔的数学功底是多么生猛,斗宗强者,恐怖如斯。
# 波函数的几率解释及两种量子力学形式的等价性
Schrödinger 试图解释波函数的物理意义:
iℏ∂t∂ψ(r)=−2mℏ2∇2ψ(r)+V(r)ψ(r)
将方程两边同乘 ψ∗(r) :
iℏψ∗(r)∂t∂ψ(r)=−2mℏ2ψ∗(r)∇2ψ(r)+ψ∗(r)V(r)ψ(r)
再将方程取复共轭后再左乘 ψ(r) 得:
−iℏψ(r)∂t∂ψ∗(r)=−2mℏ2ψ(r)∇2ψ∗(r)+ψ(r)V(r)ψ∗(r)
(1)-(2)得:
iℏ[ψ∗(r)∂t∂ψ(r)+ψ(r)∂t∂ψ∗(r)]=−2mℏ2[ψ∗(r)∇2ψ(r)−ψ(r)∇2ψ∗(r)]
两边同除 iℏ :
iℏ∂t∂[ψ∗(r)ψ(r)]=−2mℏ2∇[ψ∗(r)∇ψ(r)−ψ(r)∇ψ∗(r)]
令 ρ(r)=ψ∗(r)ψ(r) ,j(r)=−2miℏ2[ψ∗(r)∇ψ(r)−ψ(r)∇ψ∗(r)]
则方程化为流体力学中的连续性方程
∂t∂ρ(r,t)+∇⋅j(r,t)=0
Schrödinger 倾向于将 ρ(r,t) 解释为电子的质量或者电荷密度分布。若将 ρ(r,t) 视为电子质量分布,在具体例子中,经过一段时间以后,ρ(r,t) 在空间中一个很大区域内非零,即电子会变得 “越来越胖” ,这与实验结果不符合。
# Born 的波函数统计解释
ρ(r,t)=ψ∗(r,t)ψ(r,t)=∣ψ(r,t)∣2
代表在时刻 t ,在以 r为中心的一个小区域 ΔV=ΔxΔyΔz 中,找到该电子的几率密度。
若有大量粒子处于同样状态 ψ(r,t) ,在体积元 ΔV=ΔxΔyΔz 中的粒子数目就会正比于 ∣ψ(r,t)∣2ΔxΔyΔz 。
N∣ψ(r,t)∣2 解释为时刻 t 时,在空间 r处的粒子密度。
Nq∣ψ(r,t)∣2 解释为时刻 t 时,在空间 r处的电荷密度。
j(r)=−2miℏ2[ψ∗(r)∇ψ(r)−ψ(r)∇ψ∗(r)] 解释为几率流密度。
∫Ω∣ψ(r,t)∣2dr2=1<∞
ψ(r,t) 是函数空间 L2(Ω) 的一个元素,这一空间称为一个 Hilbert 空间。
集合 U={u∣u满足一些性质}
- u∈U⇒αu∈U
- u1∈U,u2∈U⇒u1+u2∈U
则集合 U 是一个线性空间。
由于 ∣ψ(r,t)∣2 是几率密度,ψ(r,t) 被称为几率幅,是不可观测量,被写作
ψ(r,t)=∣ψ(r,t)∣eiα(r,t)
eiα(r,t) 称为相位,α(r,t) 。
若有两个波函数 ψ1(r,t)=∣ψ(r,t)∣eiα1(r,t) ,ψ2(r,t)=∣ψ(r,t)∣eiα2(r,t) 仅有相位之差,则它们在物理上是等价的。
态叠加原理
设 ψ1(r,t) 和 ψ2(r,t) 分别代表体系的两个可能的运动状态,则它们的任何一个线性叠加
ψ~(r,t)=C1ψ1(r,t)+C2ψ2(r,t)
也是体系的一个可能的状态。
力学量算符的平均值(期望值):
Oˉ=∫Ωdrψ∗(r,t)O^ψ(r,t)
Schrödinger 给出动量算符和动能算符:
P^=iℏ∇=−iℏ∇,T^=−2mℏ2∇2
# Schrödinger 证明波动力学与矩阵力学的等价关系
对照 Heisenberg 的对易子
[x^,P^x]=iℏI^
在 Schrödinger 波动力学中
x^=x,P^x=iℏ∂x∂
只需要验证算符 O^≡[x^,iℏ∂x∂] 作用在任何一个波函数上,其结果都是将这个函数乘以 iℏ ,从而得到量子力学两种形式的等价性。
矩阵相等:任意向量 u∈ 线性空间 V ,使得 Au=Bu,则 A=B ,矩阵相等。
x^ϕ(r)=xϕ(r)
算符 x^ 作用在波函数上就相当于把x 读出来。
任取 ϕ(r,t) ,有
[x^,iℏ∂x∂]ϕ(r,t)=xiℏ∂x∂ϕ(r,t)−iℏ∂x∂[xϕ(r,t)]=xiℏ∂x∂ϕ(r,t)−iℏϕ(r,t)−xiℏ∂x∂ϕ(r,t)=−iℏϕ(r,t)=iℏϕ(r,t)
因此,在 Schrödinger 波动力学中,对易关系式 [x^,P^x]=iℏI^ 亦成立。
# Heisenberg 的测不准原理(不确定性原理)
关于测量:人之所以能看到物体,是因为物体直接发射或间接反射的光最终进入人眼。雷达通过电磁波发射到返回的时间来测距,根据多普勒效应来测速。对于量子体系的测量,人们倾向于选取最短的电磁波以获得 “精确”,但由于测不准原理的存在,粒子的位置测得越精确,粒子的动量就测得越不精确。
量子力学理论的一个重要问题是人们应如何理解对易关系式 [x^,P^x]=iℏI^ 的物理意义。Heisenberg 于 1927 年给出回答。
设两个力学量算符 A^、B^ 满足 [A^,B^]=iC^=0 ,即不对易。引入允许态 ψ(r^,t)( Schrödinger 方程的解,是平方可积的)
定义
AˉBˉCˉ=(ψ,A^ψ)=∫Ωdrψ∗(r^,t)A^ψ(r,t)=(ψ,B^ψ)=∫Ωdrψ∗(r^,t)B^ψ(r,t)=(ψ,C^ψ)=∫Ωdrψ∗(r^,t)C^ψ(r,t)
若 A^ ,B^ 皆为厄米算符,则
(A^−Aˉψ)ψ2⋅(B^−Bˉψ)ψ2⩾41Cˉψ2
算符 A^,B^ 不对易,则它们的均方差一定大于某个正的量,两个量不能同时测得很准,ψ 就是加权的权重,无论 ψ 怎么取,两个均方差都不能同时取很小。
(A^−Aˉψ)ψ2→0,则(B^−Bˉψ)ψ2→∞
回忆中学统计中:
| n | 1 | 2 | 3 | ⋯ | 100 |
|---|
| x | x1 | x2 | x3 | ⋯ | x100 |
xˉ=100x1+x2+x3+⋯+x100
(Δx)2=100(x1−xˉ)2+(x2−xˉ)2+(x3−xˉ)2+⋯+(x100−xˉ)2
加权:
xˉp=p1x1+p2x2+p3x3+⋯+p100x100(pi⩾0,p1+p2+⋯+p100=1)
(Δx)p2=p1(x1−xˉp)2+p2(x2−xˉp)2+p3(x3−xˉp)2+⋯+p100(x100−xˉp)2
力学量平均值:Aˉψ=(ψ,A^ψ)
内积:(ϕ,A^ψ)=∫Ωϕ∗A^ψdr(对任何一对平方可积的波函数)
∫Ωϕ∗A^ψdr≡(ϕ,A^ψ)=(B^ϕ,ψ)≡∫Ω(B^ϕ)∗ψdr⇒B^=A^†B^是A^的共轭算符(厄米共轭)
若A^†=A^,则A^ 为厄米算符。量子力学研究的所有算符都是厄米算符。
验证任意 x 和 Px 均为厄米算符
设 ψ 和 ϕ 视为算符的本征态。
(ϕ,x^ψ)=∫Ωϕ∗(x,y,z,t)[x^ψ(x,y,z,t)]dr=∫Ωϕ∗(x,y,z,t)xψ(x,y,z,t)dr=∫Ωxϕ∗(x,y,z,t)ψ(x,y,z,t)dr=∫Ω[xϕ(x,y,z,t)]∗ψ(x,y,z,t)dr=∫Ω[x^ϕ(x,y,z,t)]∗ψ(x,y,z,t)dr=(x^ϕ,ψ)
x^ψ=xψ ,算符起到的作用就是把一个数读出来。
x^=x^† ,无条件的厄密。
(ϕ,P^xψ)=∫Ωϕ∗(x,y,z,t)[P^xψ(x,y,z,t)]dr=∫Ωϕ∗(x,y,z,t)iℏ∂x∂ψ(x,y,z,t)dr=iℏ∫Ωϕ∗(x,y,z,t)∂x∂ψ(x,y,z,t)dr=iℏ{[ϕ∗ψ]∣−∞∞−∫[∂x∂ϕ]∗ψdr}=iℏϕ∗ψ∣−∞∞−iℏ∫[∂x∂ϕ]∗ψdr=iℏϕ∗ψ∣−∞∞+∫(iℏ∂x∂ϕ)∗ψdr=iℏϕ∗ψ∣−∞∞+∫(P^xϕ)∗ψdr=iℏϕ∗ψ∣−∞∞+(P^xϕ,ψ)=(P^xϕ,ψ)
P^x=iℏ∂x∂
分部积分:若函数 u(x) 和 v(x) 在区间 I 上有连续导数,则有分部积分公式( x∈I ):
∫uv′dx=uv−∫u′vdx
或
∫udv=uv−∫vdu
∣−∞∞亦可写成∣∂Ω,∂Ω在边界上
正交:ϕ∗ψ∣∂Ω≡0
P^x=P^x† ,有条件的厄密,即在边界上是厄密的。
引入 F(ξ)=∫Ω∣∣∣∣ξA^ψ+iB^ψ∣∣∣∣2dr(⩾0)
展开为
∫Ω(ξA^ψ+iB^ψ)∗(ξA^ψ+iB^ψ)dr=∫Ω[ξ(A^ψ)∗−i(B^ψ)∗][ξ(A^ψ)−i(B^ψ)]dr=∫Ω[ξ2(A^ψ)∗(A^ψ)−iξ(B^ψ)∗(A^ψ)+iξ(A^ψ)∗(B^ψ)+(B^ψ)∗(B^ψ)]dr=ξ2(ψ,A^2ψ)+i∫Ωξ(A^ψ)∗(B^ψ)dr+(ψ,B^2ψ)−i∫Ω(B^ψ)∗(A^ψ)dr=ξ2∫Ωψ∗A^2ψdr+∫Ωψ∗B^2ψdr+iξ(A^ψ,B^ψ)−iξ(B^ψ,A^ψ)
∫Ωξ2(A^ψ)∗(A^ψ)dr=ξ2(A^ψ,A^ψ)=ξ2(A^†ψ,A^ψ)=ξ2(ψ,A^(A^ψ))
ξ2∫Ωψ∗A^2ψdrξ2∫Ωψ∗B^2ψdr=ξ2(ψ,A^2ψ)=ξ2(ψ,B^2ψ)
因为
iξ(A^ψ,ψB^)=iξ(A^†ψ,B^ψ)=iξ(ψ,A^B^ψ)−iξ(B^ψ,ψA^)=−iξ(B^†ψ,A^ψ)=−iξ(ψ,B^A^ψ)
所以原式
∫Ω∣∣∣∣ξA^ψ+iB^ψ∣∣∣∣2dr=ξ2(ψ,A^2ψ)+(ψ,B^2ψ)+iξ(ψ,A^B^ψ)−iξ(ψ,B^A^ψ)=ξ2(ψ,A^2ψ)+(ψ,B^2ψ)+iξ[(ψ,A^B^ψ)−(ψ,B^A^ψ)]=ξ2(ψ,A^2ψ)+(ψ,B^2ψ)+iξ(iCψ)=ξ2Aψ2+Bψ2−ξCψ
(ψ,A^B^ψ)−(ψ,B^A^ψ)=∫Ωψ∗A^B^ψdr−∫Ωψ∗B^A^ψdr=∫Ωψ∗(A^B^−B^A^)ψdr=∫Ωψ∗[A^,B^]ψdr=∫Ωψ∗iC^ψdr=i∫Ωψ∗C^ψdr=iCψ
F(ξ)=ξ2Aψ2+Bψ2−ξCψ(⩾0)
ξmin=2Aψ2Cψ,F(ξmin)=(2Aψ2Cψ)2Aψ2+Bψ2−(2Aψ2Cψ)Cψ=Bψ2−41Aψ2Cψ(⩾0)
Aψ2⋅Bψ2⩾41(Cψ)2
Aψ2=(ψ,A^2ψ)=(ψ,A^A^ψ)=(A^†ψ,A^ψ)=(A^ψ,A^ψ)=∫Ω(A^ψ)∗(A^ψ)dr=∫Ω∣∣∣∣A^ψ∣∣∣∣2dr
引入 A~=A^−AψI^,B~=B^−BψI^ ,
[A~,B~]=[A^−AψI^,B^−BψI^]=[A^ψ,B^ψ]=iCψ
Aψ2⋅Bψ2⩾41(Cψ)2⇒(A^−Aψ)2⋅(B^−Bψ)2⩾41(Cψ)2
令 A^=x^,B^=P^x
[x^,P^x]=iℏI^⇒C^=ℏI^
则
(Δx^)2⋅(ΔP^x)2⩾41C2=41ℏ2
利用测不准原理说明氢原子最低能量态(基态)的存在(即回答卢瑟福的问题:为什么原子是稳定的?)
求最小值,即电子与原子核距离极近。
rˉ∽0∽(Δr)2,Pˉ∽0∽(ΔP)2(r很小时,均值近似于均方差值,开方是为了统一量纲)
(ΔP)2⋅(Δr)2(ΔP)2⋅r2ˉ(ΔP)2∽41ℏ2∽41ℏ2∽4ℏ2r2ˉ1
E(r)≅2mP2−rˉe2≅2m(ΔP)2−rˉe2≅2m14ℏ2r2ˉ1−rˉe2
drdrˉmin=8mℏ2(−2)r3ˉ1+r2ˉe2=0极小值导数为0=4me2ℏ2
E(r)⩾E(rˉmin)=Emin=−ℏ22me4
Landau 书中说,测不准原理表明,量子力学从本质上是不同于经典力学规律的。一般的经典理论自身都是完备的,并不依赖于它们各自的极限理论,但人们却不能在将经典力学抛在一边的情况下去构造量子力学的理论框架(前者是后者在 ℏ→0 下的近似)。这是因为,在量子力学理论中,一切有意义的物理量都是所谓的可观测量,这就要求:为了描述粒子的运动,除了保证该粒子本身的存在之外,还必须存在有被称之为 “仪器” 的物体存在,而后者的动力学是由经典物理学加以支配的。量子力学理论实际上告诉我们的是:一个量子客体是如何与经典物体(仪器)相互作用的。当一个量子客体与 “仪器” 相互作用时,两者的状态都会发生变化。这是哥本哈根学派量子理论的基础。量子力学在物理理论中占据着一个十分特殊的地位。它不仅将经典力学作为它的极限理论,同时它也需要经典力学来构建自身。
例题[简答题]
定义一个粒子的轨道角动量算符为
L^=r×P=(yPz−zPy)i+(zPx−xPz)j+(xPz−zPx)k
利用对易关系
[x^,P^x]=[y^,P^y]=[z^,P^z]
证明
[L^x,L^y]=iℏL^z,[L^y,L^z]=iℏL^x,[L^z,L^x]=iℏL^y
参考答案
证明:
[L^x,L^y]=L^xL^y−L^yL^x=(y^P^z−z^P^y)(x^P^z−z^P^x)−(z^P^x−x^P^z)(z^P^y−y^P^z)=y^P^zx^P^z−y^P^zz^P^x−z^P^yx^P^z+z^P^yz^P^x−z^P^xz^P^y+z^P^xy^P^z+x^P^zz^P^y−x^P^zy^P^z=P^zz^y^P^x+z^P^zx^P^y−z^P^zy^P^x−P^zz^x^P^y=(z^P^z−P^zz^)(x^P^y−y^P^x)=iℏL^z
z^P^xz^P^y−z^P^yz^P^x=[z^P^x,z^P^y]=z^[P^x,z^P^y]+[z^,z^P^y]P^x=z^2[P^x,P^y]+z^[P^x,z^]P^y+z^[z^,P^y]P^x+[z^,z^]P^xP^y=0
x^P^zy^P^z−y^P^zx^P^z=[x^P^z,y^P^z]=x^[P^z,y^P^z]+[x^,y^P^z]P^z=x^y^[P^z,P^z]+[x^,y^]P^zP^z+x^[P^z,y^]P^z+y^[x^,P^z]P^z=0
# 参考资料